Probabilidades de la ruleta y ventaja de la casa: Un análisis matemático

La ruleta es uno de los juegos de casino más antiguos y el más sencillo de entender y jugar. No necesitas conocimientos avanzados de matemáticas para comprender las probabilidades de la ruleta y otras nociones matemáticas aplicadas en este juego y sus estrategias.
Inventado por el matemático Blaise Pascal (el primer padre de la teoría de probabilidades) en el siglo XVIII, también es el juego de casino más simple con respecto a los cálculos de probabilidades en la ruleta.
Jugado en su forma contemporánea durante más de 220 años, podemos otorgar a la ruleta otro superlativo además de la simplicidad, a saber, la transparencia.
En este juego, los posibles resultados son visibles y contables en la rueda de la ruleta. Es posible calcular las probabilidades de ganar cualquier apuesta en particular (a diferencia de otros juegos de azar, como las máquinas tragamonedas).
Ten en cuenta
A pesar de tales virtudes, la ruleta es todavía un juego en el que muchos jugadores caen en la trampa de creencias falsas o irracionales, falacias y conceptos erróneos.
Tales situaciones pueden evitarse cuando los jugadores conocen los hechos matemáticos detrás de la ruleta y son conscientes de la posibilidad de interpretarlos incorrectamente.
Esta guía te familiarizará con las probabilidades de la ruleta, las probabilidades de pago y la ventaja de la casa, proporcionando una fuente confiable para sus valores numéricos.
La guía cubre las versiones más populares de la ruleta: americana, europea y francesa.
Aquí aprenderás:
- Apuestas simples y combinadas y sus probabilidades de pago
- Probabilidades básicas de la ruleta
- Probabilidades de ganar una apuesta combinada
- Cómo aumentar las probabilidades de ganar en la ruleta
- Probabilidades de resultados repetidos
- Explicación de la ventaja de la casa en la ruleta
- Cómo cambia la ventaja de la casa en la ruleta con las reglas
Empecemos.
Apuestas simples y combinadas en la ruleta y sus probabilidades de pago
Primero, debes saber que no hay mucha diferencia entre las tres versiones de la ruleta en cuanto a reglas y tabla de pagos.
Estas versiones difieren en el diseño de la mesa de apuestas y el número adicional (00) que la ruleta americana tiene en su rueda y mesa.
Sin embargo, las probabilidades asociadas con las apuestas y las ventajas de la casa son diferentes en cada versión, como veremos en una sección posterior.
Una apuesta simple en la ruleta se define como una apuesta realizada mediante una única colocación de fichas en la mesa de ruleta.
Por ejemplo, una apuesta dividida es una apuesta simple hecha mediante una colocación de fichas en el borde común de dos cuadrados contiguos en la mesa; como en el 4 y 5, o 6 y 9, y así sucesivamente.
Hay dos categorías de apuestas simples: apuestas internas y apuestas externas. El nombre se refiere a la posición de la zona marcada para la apuesta en la mesa en relación con la cuadrícula de números.
Las probabilidades de pago son la tasa a la que la apuesta simple que ganas se te paga junto con tu apuesta inicial y se expresan en forma de probabilidades.
Por ejemplo, las probabilidades de pago de una apuesta de columna son 2:1, lo que significa que se te paga el doble de tu apuesta si ganas.
Hay 10 tipos de apuestas simples, que se enumeran en las tablas a continuación junto con sus probabilidades de pago y el número posible de colocaciones:
Las probabilidades de pago anteriores se aplican a cualquiera de las tres versiones de la ruleta.
Las apuestas de trío y cuatro números son específicas de la ruleta francesa. Sin embargo, varios casinos permiten tales apuestas en la ruleta europea o americana.
En la fila de dividida, el número depende de las reglas de cada casino respecto a una apuesta dividida con el número 0 o 00.
Por ejemplo
Si apuestas $10 en una calle, tienes 12 opciones posibles para colocar tus fichas en la mesa, y si ganas, se te paga $10 x 11 = $110 más tu apuesta inicial.
Una apuesta combinada (o compleja) es una apuesta hecha de varias colocaciones simultáneas, cada una con su propia apuesta, según las reglas de colocación. Por lo tanto, una apuesta combinada consiste en varias apuestas simples.
Para una apuesta combinada, el pago se aplica de la siguiente manera: las apuestas simples que se pierden no reciben premio, y pierdes sus apuestas y para cada apuesta simple que se gana se aplican sus probabilidades de pago, según la tabla anterior.
Por ejemplo
Supón que colocaste una apuesta combinada en la ruleta europea, que consiste en las siguientes apuestas simples: $10 en Rojo, $2 en calle (10, 11, 12), y $1 en apuesta plena al número 21.
Supongamos que sale el número 12. Pierdes la apuesta plena y recuperas $10 x 1 + $10 + $2 x 11 + $2 = $44, lo que significa una ganancia de $32 en esta apuesta.
Ten en cuenta
El pago se refiere a la ganancia que obtienes cuando una apuesta se gana y no a la cantidad total de dinero que recibes del crupier. Esta última también incluye tu apuesta inicial.
Probabilidades básicas de la ruleta
Las probabilidades de los diversos resultados pueden calcularse utilizando la fórmula clásica de probabilidad:
“La probabilidad de un evento es la proporción entre el número de situaciones favorables para que ocurra ese evento y el número total de situaciones igualmente posibles.”
Esto significa una operación aritmética simple, la de la división.
Cada número en la rueda de la ruleta representa un evento elemental y todos estos eventos son igualmente posibles en una tirada aleatoria de la rueda. En términos de teoría de la probabilidad, estos números forman el espacio muestral del experimento de girar la rueda de la ruleta.
Como tal, la probabilidad de que ocurra un número específico es 1 dividido por el total de números en la rueda, es decir:
- 1/37 (2.70%) para la ruleta europea o francesa
- 1/38 (2.63%) para la ruleta americana.
¿Qué pasa con la probabilidad de eventos compuestos?
Un evento compuesto consiste en una unión (disyunción) de varios eventos elementales.
Por ejemplo
El evento E: “cualquiera de los números 22, 23, 25 y 26” en una ruleta europea consiste en cuatro eventos elementales (se identifica con el conjunto {22, 23, 25, 26}) y su probabilidad es P(E) = 4/37 (10.81%). El evento E es en realidad el evento de ganar la apuesta de esquina en los números (22, 23, 25, 26).
En la tabla a continuación se anotan las probabilidades de ganar para cada una de las apuestas simples de la ruleta en formato fraccional, porcentual y de probabilidades.
Ejemplos
- Una apuesta simple a los números 32 y 35 en la ruleta americana es una apuesta dividida y tiene una probabilidad de ganar del 5.26%;
- Una apuesta simple a los números del 1 al 12 en la ruleta europea es una apuesta a docena (1ª docena) y tiene una probabilidad de ganar del 32.43%;
- Una apuesta simple al rojo en la ruleta francesa es una apuesta de color y tiene una probabilidad de ganar del 48.64%.
Podemos ver en esta tabla que las probabilidades de ganar son las mismas para la ruleta europea y la francesa (y esto es obvio, ya que las dos versiones tienen el mismo espacio muestral) y que las probabilidades de ganar para la ruleta europea/francesa son ligeramente superiores a las de la ruleta americana.
La principal diferencia entre las ruedas de ruleta proviene, por supuesto, del hecho de que la americana tiene un número más en la rueda (el doble cero).
Al observar las probabilidades de las apuestas simples, se puede ver que aumentan con las apuestas externas y alcanzan su máximo para las apuestas rojo/negro, par/impar y bajo/alto (47.36% - 48.64%).
Parecen altas probabilidades de ganar que no encontramos en otros juegos de casino, pero no te emociones por esto: Las probabilidades de ganar no son lo único que cuenta al describir una apuesta, como veremos en una sección posterior.
Probabilidades de ganar en la ruleta con una apuesta combinada
Las reglas de la ruleta permiten múltiples colocaciones por toda la mesa y en cualquier combinación, resultando en apuestas combinadas. Calcular la probabilidad de ganar una apuesta de este tipo es tan simple como hacerlo para las apuestas simples.
El conjunto de números sobre los que se realiza una apuesta (simple o combinada) se llama la cobertura de esa apuesta (C).
Ejemplos
- Una apuesta de calle simple a los números 16, 17 y 18 tiene la cobertura {16, 17, 18}, contando tres elementos (números);
- Una apuesta simple al negro tiene la cobertura {2, 4, 6, 8, 10, 11, 13, 15, 17, 20, 22, 24, 26, 28, 29, 31, 33, 35}, contando 18 elementos;
- Una apuesta combinada que consiste en una apuesta dividida a (22, 25) y una apuesta a la 2ª docena tiene la cobertura {13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25}, contando 13 elementos.
La probabilidad de ganar una apuesta combinada B es la relación entre la cardinalidad de su cobertura (el número de elementos en el conjunto de cobertura o la longitud de la cobertura) y el número total de números (37 o 38): P(B) = |C(B)|/37 o P(B) = |C(B)|/38, dependiendo de la versión de la ruleta.
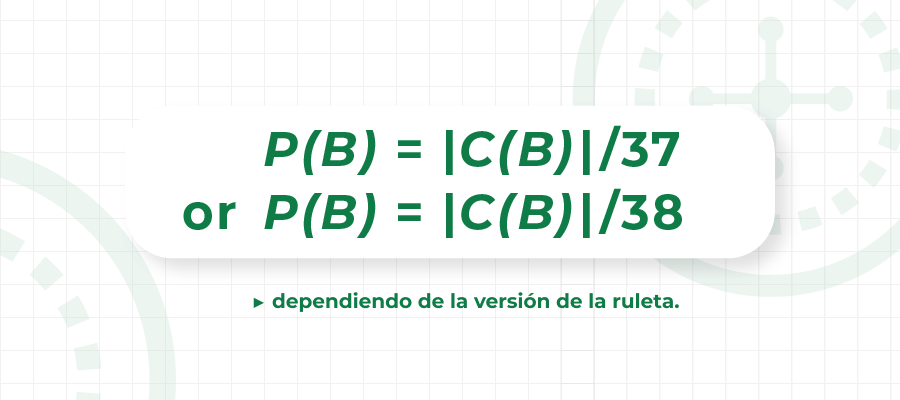
Ejemplo rápido
Tomemos una apuesta B en la ruleta europea que consiste en las apuestas divididas a (4, 5) y (5, 6) y la apuesta a la 2ª Columna. La cobertura de B es C(B) = {2, 4, 5, 6, 8, 11, 14, 17, 20, 23, 26, 29, 32, 35}, contando 14 elementos, su cardinalidad es |C(B)| = 14, entonces la probabilidad de ganar B es P(B) = 14/37 = 37.83%, mientras que la probabilidad de perder es 1 – P(B) = 62.17%.
Ten en cuenta
Al calcular la probabilidad de ganar una apuesta combinada, primero establece su cobertura haciendo la unión de todas las coberturas de las apuestas simples constituyentes. Para contar la cardinalidad de la cobertura de la apuesta, debes contar cada elemento solo una vez. Algunas coberturas pueden superponerse (como en el ejemplo anterior) y cualquier número cuenta igual para la probabilidad.
Observando la fórmula anterior de probabilidad, se puede concluir que cuanto mayor sea la cobertura de una apuesta, mayor será su probabilidad de ganar.
Pero esto no significa que esparcir las fichas caóticamente en la mesa solo para cubrir tantos números como sea posible sea una acción de apuesta sensata.
Hay 2 razones para esto:
- Podríamos encontrar una apuesta que nunca gane, sin importar el resultado del giro.
Por ejemplo: Si apuestas la misma cantidad, digamos, $1 en cada uno de los 38 números de una ruleta americana (38 apuestas directas), esta apuesta combinada tendría un beneficio negativo de $1 x 35 – $1 x 37 = – $2, cualquiera que sea el resultado del giro. Esto es cierto porque solo una apuesta directa gana y las otras 37 pierden.
O, si apuestas $1 en cada número del 1 al 18 y $18 en Alto, entonces: si ocurre un número del 1 al 18, tu beneficio sería $1 x 35 – $1 x 17 – 1 x $18 = 0; si ocurre un número alto, tu beneficio sería – 1 x $18 – 18 x $1 = – $36, lo cual es negativo.
Estas apuestas combinadas que resultan en una pérdida, cualquiera que sea el resultado, se llaman apuestas contradictorias y deben evitarse, independientemente de su cobertura.
- Alta probabilidad de ganar no implica mayores ganancias.
En la matemática de la ruleta, el posible beneficio de una apuesta se describe por la función de beneficio de esa apuesta, que iguala los pagos de las apuestas constituyentes.
La ruleta es un juego concebido de tal manera que existe un equilibrio entre la probabilidad de ganar y el posible beneficio de una apuesta en relación con la apuesta – cuanto mayor es uno, menor es el otro.
Este equilibrio tiene, por supuesto, el papel de garantizar la ventaja de la casa y minimizar el riesgo de que la casa quiebre.
Ten en cuenta
No coloques una apuesta combinada con una gran cobertura sin verificar si la apuesta no es contradictoria.
Mejorando las probabilidades de ganar en la ruleta
Cuando se habla de mejorar las probabilidades de ganar en un giro de ruleta, se trata de realizar apuestas combinadas que ofrezcan una mayor probabilidad de ganar que las apuestas simples.
Dado que la probabilidad de ganar aumenta con la cobertura de una apuesta, elegir una gran cobertura es el único medio por el cual se pueden obtener mayores probabilidades de ganar.
Este principio también se aplica en otros juegos de azar (por ejemplo, habilitar más líneas de pago en las tragamonedas o comprar más boletos en la lotería aumenta las probabilidades de ganar).
La ruleta es el juego de casino que proporciona las mayores probabilidades de ganar para apuestas estratégicas. Consulta nuestra guía para principiantes si aún no estás familiarizado con todas las apuestas y combinaciones.
Las apuestas combinadas con gran cobertura pueden llegar a alcanzar más del 92% de probabilidades de ganarlas y obtener beneficios. Sin embargo, como ya he dicho, la probabilidad de ganar no es el único factor en la ecuación de ganar en la ruleta.
Elegir las apuestas combinadas que colocar no puede hacerse de manera caótica. Vimos que un primer requisito es que la apuesta no sea contradictoria, por lo que se necesita verificar su posible beneficio.
Segundo, no hay una razón objetiva para elegir las apuestas constituyentes de tal manera que su cobertura se superponga, es decir, que tengan números cubiertos por más de una apuesta. En la teoría de la ruleta, se ha demostrado que cualquier apuesta combinada es equivalente a una apuesta combinada. Esto significa que tienen la misma longitud de su cobertura y los mismos valores de sus funciones de beneficio) cuyas apuestas constituyentes no se superponen en cobertura (una apuesta así se llama apuesta disjunta).
El razonamiento estratégico para elegir una apuesta disjunta entre dos apuestas equivalentes es el siguiente:
Con esta elección, podemos ahorrar una parte del total de la apuesta para otra apuesta que se realizará en el mismo giro o para un giro futuro mientras mantenemos la misma probabilidad de ganar entre las dos apuestas.
Se trata de ahorrar dinero en relación con las probabilidades de ganar en la ruleta.
Ten en cuenta
Para un giro, elegir apuestas que no se superpongan en cobertura es mejor.
Tercero, la ampliación de la cobertura debe hacerse en relación con tu estrategia de apuestas, que también involucra la gestión del saldo. Una probabilidad de ganar alta siempre se contrarresta con una tasa de beneficio baja, para que la ventaja de la casa a largo plazo esté asegurada.
Por ejemplo
En una ruleta americana, supongamos que colocas la siguiente apuesta combinada: $23 al rojo y $1 a cada uno de los 12 números negros. Las probabilidades generales de ganar esta apuesta de gran cobertura son alrededor del 79%. Si ganas la apuesta de color, el beneficio es de $11, y si ganas una apuesta directa, el beneficio es de solo $0.5. Si pierdes todas las apuestas (con aproximadamente un 21% de probabilidades), la pérdida es de $35.
Podemos ver que el posible beneficio es relativamente bajo si consideramos la inversión de $35.
La tasa de ganancias de una apuesta es la relación entre su apuesta y la ganancia promedia posible en caso de ganar y cuenta como otro factor en las decisiones de apuestas junto con la probabilidad.
Existen varias estrategias de apuestas con grandes coberturas combinadas, cumpliendo todos o la mayoría de los requisitos anteriores.
Algunas apuestas de gran cobertura conocidas están en las siguientes categorías:
- Apostar a un color y a números del color opuesto
- Apostar a una columna y a números fuera de esa columna
- Apostar a la tercera columna y al color negro
- Apostar a calles y al opuesto del color predominante
- Apostar a esquinas y al opuesto del color predominante
- Apostar a líneas y al opuesto del color predominante
- Apostar a un color y a divisiones del color opuesto
- Apostar a bajo/alto y a divisiones de números bajos/altos
- Apostar a la primera y tercera columnas y al color negro.
Cada una de estas apuestas combinadas se caracteriza por parámetros que dan las probabilidades de ganar y perder y la tasa de ganancia. Antes de elegir una apuesta de este tipo, vale la pena conocer estos indicadores matemáticos para ver si se ajusta a tus objetivos y estrategia de apuestas, incluida la gestión del dinero.
Por ejemplo, considera en la lista anterior la apuesta combinada 'a la tercera columna y al color negro' en la ruleta americana. Esta apuesta deriva de la observación de que la tercera columna contiene más números rojos que cualquiera de las otras dos. Al combinar la apuesta a columna (a la tercera columna) con una apuesta al color negro, ampliamos la cobertura e implícitamente aumentamos la probabilidad de ganar. El único parámetro que caracteriza esta apuesta es la relación entre la apuesta al color y la de la columna (denótalo por c).
Recuerda
Bajo la condición de un beneficio no negativo en los casos no perdidos, algunas matemáticas simples dan una limitación para el parámetro c, al restringirlo a tomar valores en el intervalo [1, 2].
La siguiente tabla nota las probabilidades y beneficios posibles para esta apuesta, para los diversos valores de c en incrementos de 0.2. La letra S denota la apuesta a la columna:
Con una probabilidad de ganar del 68.43%, este tipo de apuesta con dos colocaciones ofrece tasas de ganancia relativamente buenas para el posible beneficio.
Su probabilidad de ganar es aproximadamente un 20% mayor que la de una apuesta de color, por ejemplo, cuya tasa de beneficio es aproximadamente la misma que la tasa promedio de la apuesta combinada. Estas ventajas sobre la apuesta de color se contrarrestan, sin embargo, con una posible pérdida mayor para la apuesta combinada.
Probabilidades de resultados repetidos
En las secciones anteriores, hemos tratado con las probabilidades asociadas con apuestas estáticas, es decir, apuestas realizadas en una sola tirada. Un comportamiento de apuesta frecuente de muchos jugadores es mantener la misma apuesta durante varias tiradas, con una cantidad constante o creciente. Esta última opción está relacionada con sistemas de apuestas progresivas como el Martingala.
Para tales apuestas, uno puede estar interesado en cuál es la probabilidad de una cierta sucesión de resultados del mismo tipo o la probabilidad de un cierto número de resultados del mismo tipo ocurriendo dentro de un número dado de tiradas.
Consideremos un evento A dado por el resultado esperado de una apuesta simple (por ejemplo, color rojo, número alto, número 15, 1ª columna, y así sucesivamente). Después de cada tirada, el evento A puede ocurrir con probabilidad p y no ocurrir con probabilidad 1 – p.
Dado que las tiradas son independientes, también lo son las ocurrencias del evento A. Entonces, la probabilidad de que A ocurra n veces seguidas es simplemente la multiplicación:
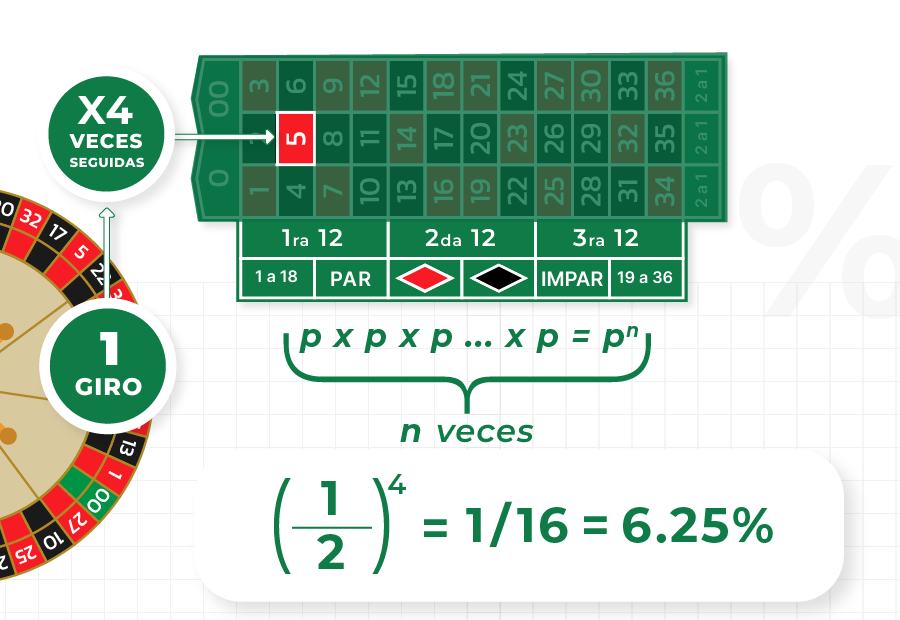
Por ejemplo
Para calcular la probabilidad de que ocurra un número rojo cuatro veces seguidas, toma la probabilidad de que ocurra en una tirada y elévala a la potencia de 4: Vamos a aproximar su probabilidad en una tirada a 1/2, para simplificar el cálculo (la probabilidad real es 48.64% o 47.36%, dependiendo de la versión de la ruleta). Entonces, la probabilidad buscada es aproximadamente 6.25%.
Dado que p es un número menor que 1, se sigue que cuanto más larga sea la sucesión, menor será su probabilidad. De hecho, la probabilidad disminuye exponencialmente con el número de tiradas.
La probabilidad de tener cinco rojos seguidos es 3.12%, y tener ocho rojos seguidos se reduce a 0.39%.
Estas probabilidades bajas para las repeticiones alimentan una falacia de juego bien conocida, basada en la creencia de que tal sucesión tiene que terminar rápidamente para que la aleatoriedad se "restablezca" de alguna manera.
Tal creencia induce una estimación incorrecta de la probabilidad de un nuevo resultado del mismo tipo (continuando la sucesión) a ser menor de su probabilidad real. Esta falacia se llama la falacia de Monte Carlo y afecta especialmente a aquellos que juegan sistemas de apuestas progresivas.
La actitud correcta en relación con los resultados repetidos es saber que cada tirada es independiente de la anterior y que la probabilidad de un resultado siempre es la misma, independientemente de las ocurrencias previas.
Por ejemplo, la probabilidad de que ocurra un número rojo en la siguiente tirada es aproximadamente 1/2, sin importar cuán larga sea la sucesión de rojos hasta esa tirada.
La probabilidad de que el evento A ocurra exactamente m veces en n tiradas se da por una fórmula un poco más compleja, donde el primer factor es el número de combinaciones de n elementos tomados cada m:
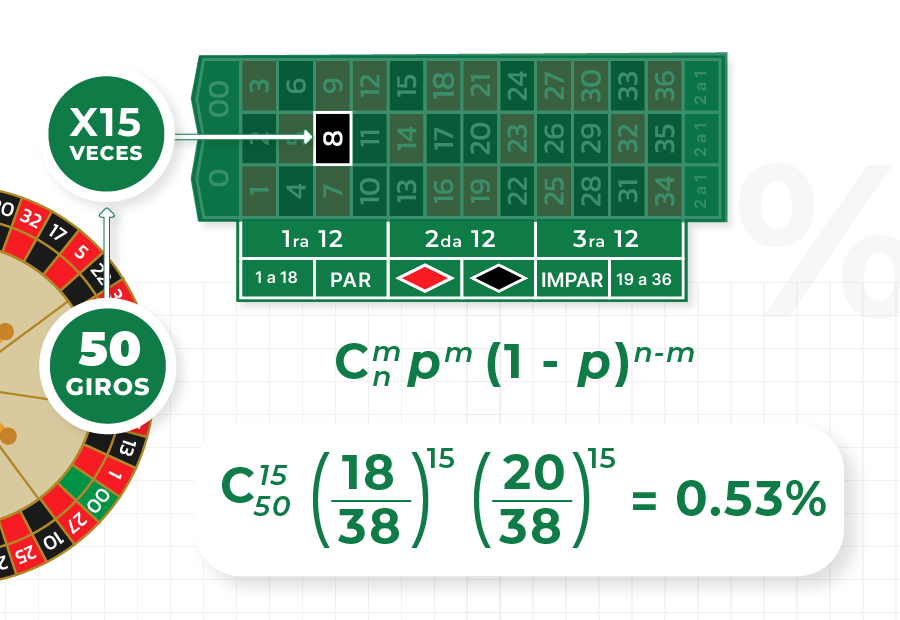
Como se puede ver en la imagen de arriba, en la ruleta americana, la probabilidad de que ocurra un número negro 15 veces en 50 tiradas es 0.53%.
En la ruleta americana, la probabilidad de que ocurra un número rojo al menos 7 veces en 10 tiradas se calcula de la siguiente manera: tenemos que aplicar la fórmula anterior cuatro veces, es decir, para m = 7, m = 8, m = 9, y m = 10, y sumar los resultados. Esta operación nos da una probabilidad de 13.21%.
Ten en cuenta
Cada resultado es independiente del anterior y la probabilidad de un resultado no depende de los resultados anteriores ni de la probabilidad de que ocurran en sucesión.
Explicación de la ventaja de la casa en la ruleta
Las probabilidades asociadas con una apuesta, junto con sus cuotas de pago, dan lo que se llama la expectativa matemática o valor esperado de esa apuesta.
En otras palabras, la cantidad promedio a ganar o perder a largo plazo con esa apuesta.
En general, el valor esperado (VE) de una apuesta se define de la siguiente manera:
(probabilidad de ganar) × (ganancia si ganas) + (probabilidad de perder) × (pérdida si pierdes).
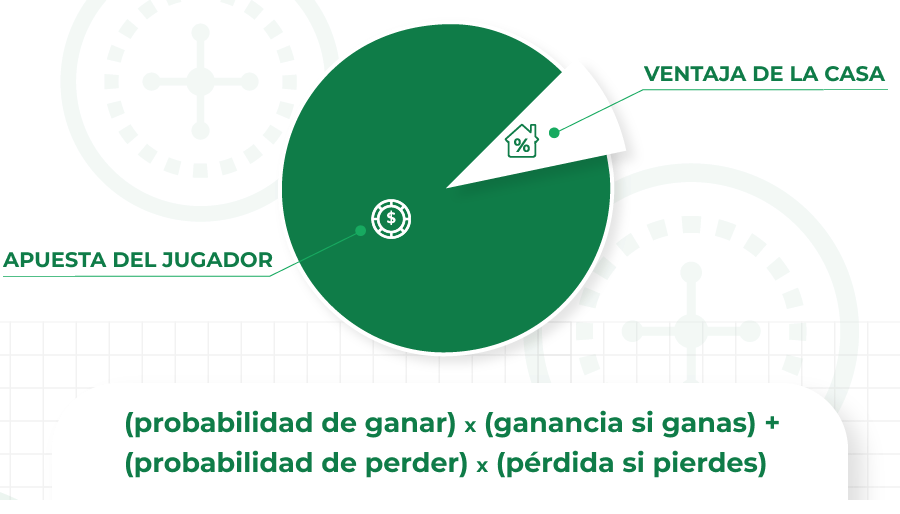
Por ejemplo, una apuesta a una columna con una cantidad de $3 en la ruleta europea tiene una expectativa de: 12/37 × $6 ˗ 25/37 × $3 = ˗8.1 centavos.
Esta fórmula emplea las probabilidades de ganar y no ganar la apuesta, el pago de la apuesta (2 a 1 para la apuesta a columna) y la cantidad apostada. El resultado se lee de la siguiente manera: si uno realiza esta apuesta un número suficientemente grande de veces, se espera que pierda en promedio 8.1 centavos por cada tres dólares apostados o 2.7 centavos por cada dólar apostado.
En teoría de probabilidades, ese "promedio" significa un límite y no realmente una media aritmética; es un promedio estadístico.
La ventaja de la casa (HE) de una apuesta se define como el opuesto (como signo positivo o negativo) de su valor esperado. HE se expresa como un porcentaje y se calcula como la proporción de la pérdida promedio respecto a la apuesta inicial. HE expresa la tasa de ganancia que la casa obtiene a largo plazo de las pérdidas de los jugadores.
HE también es específica para un juego, no solo para cada apuesta en ese juego, y se calcula como un promedio estadístico para todas las apuestas en ese juego.
En nuestro ejemplo de apuesta a columna en la ruleta europea, HE es 2.70%.
Si considera cualquier otra apuesta para el cálculo (número completo, división, calle, etc.) encontrará el mismo 2.70% para la ruleta europea.
Esto sucede porque la tabla de pagos de la ruleta está diseñada para mantener la misma ventaja de la casa en todas las apuestas.
Esto no sucede en todos los juegos de casino. La mayoría de ellos tienen diferentes ventajas de la casa para sus apuestas. Es otro elemento de simplicidad para el juego de la ruleta.
Ten en cuenta
La ventaja de la casa en la ruleta americana es casi el doble que la HE de la ruleta europea; es 5.26%. HE es mayor debido al número adicional 00 que tiene la ruleta americana en su rueda.
Esta diferencia en HE se convierte en una recomendación directa de elegir la ruleta europea o francesa en lugar de la ruleta americana.
Si tomamos como criterio de elección las probabilidades de ganar, la diferencia seguirá favoreciendo a la ruleta europea, pero no tan significativamente:
Para una apuesta a número completo, la diferencia en probabilidad de ganar es 1/37 - 1/38 = 0.00071 = 0.071%, lo cual es insignificante.
La diferencia aumenta con la cobertura de la apuesta: para una apuesta a calle, 3/37 - 3/38 = 0.21%; para una apuesta a línea, 6/37 - 6/38 = 0.43%; para una apuesta a docena, 12/37 - 12/38 = 0.86%, alcanzando su máximo para una apuesta a color, par/impar, o baja/alta, es decir, 18/37 - 18/38 = 1.28%.
Aún no es mucho, pero estos últimos tipos de apuestas son los que más se ven afectados por el cero y doble cero, y para la ruleta americana, las probabilidades de perder tal apuesta se casi duplican.
Esa diferencia de 1.28% aumenta aún más para apuestas combinadas con alta cobertura. Por ejemplo, una apuesta combinada no contradictoria consistente en una apuesta a alta y diecisiete apuestas iguales a números completos bajos tiene una probabilidad de 94.59% en la ruleta europea y 92.10% en la ruleta americana, por lo que la diferencia saltó a 2.49%.
La única razón práctica para elegir la ruleta americana no estaría basada en HE o probabilidad, sino más bien en las reglas particulares de apuestas del casino.
Una de esas reglas sería la permisión de apuestas más bajas para ciertos tipos de apuestas en algunos casinos de ruleta americana.
Recuerda
La ruleta europea ofrece mayores probabilidades de ganar para la misma apuesta y una ventaja de la casa menor que la ruleta americana.
Cómo cambia la ventaja de la casa en la ruleta con las reglas
En la ruleta, la ventaja de la casa no puede reducirse usando ciertas estrategias de apuestas.
Esto es posible en el blackjack, donde las estrategias óptimas reducen la ventaja regular de la casa, así como en otros juegos de azar que permiten el juego óptimo.
En la ruleta, la ventaja de la casa permanece fija y solo puede variar con las reglas del juego que determinan las versiones de este juego.
Hay dos reglas que impactan la ventaja de la casa.
Estas reglas son específicas principalmente de la ruleta francesa, pero algunos casinos también las incluyen para otros tipos de ruleta. Estas reglas se aplican cuando la bola cae en el bolsillo del cero:
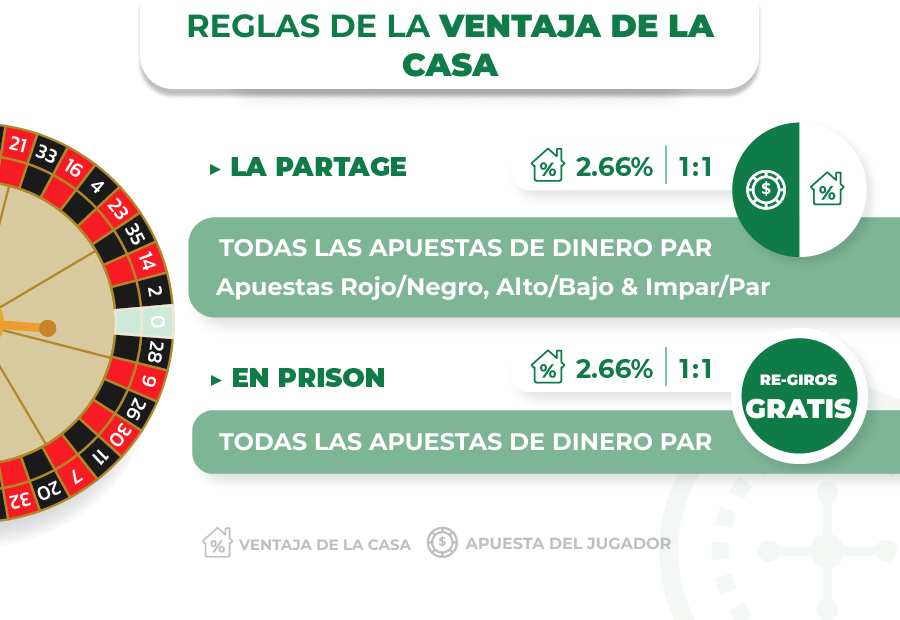
La regla de La Partage establece que si la bola cae en el bolsillo del cero, todas las apuestas de dinero par (para rojo/negro, alto/bajo, y par/impar) se dividen automáticamente por la mitad.
La mitad de la apuesta original se devolverá al jugador mientras que la casa toma la mitad restante.
La regla de En Prison establece que para una apuesta de dinero par, si la bola cae en cero, la apuesta se congela y una nueva tirada gratuita determinará si la apuesta se gana o se pierde.
La regla de La Partage y En Prison solo se aplican a las apuestas de dinero par (cuotas de pago 1:1) y no están presentes ambas en un juego.
Para tales apuestas, la ventaja de la casa es 1.35% en lugar de 2.70%.
Esta ventaja de la casa es solo para ese tipo de apuesta para la cual se aplica una de las dos reglas anteriores; para el resto de las apuestas, la misma ventaja de la casa de 2.70% se mantiene.
Por lo tanto, la ventaja general de la casa del juego no se reduce a 1.35%.
Asumiendo una distribución uniforme de los tipos de apuestas a lo largo del tiempo, la ventaja de la casa de una ruleta francesa con una de las reglas La Partage o En Prison es 2.66%.
| APUESTA | VENTAJA DE LA CASA |
|---|---|
| Cualquier apuesta en la ruleta europea clásica | 2.70% |
| Cualquier apuesta en la ruleta americana clásica | 5.26% |
| Apuesta no igualada en la ruleta francesa | 2.70% |
| Apuesta igualada en la ruleta francesa con La Partage o En Prison | 1.35% |
| VERSIÓN DE LA RULETA | VENTAJA GENERAL DE LA CASA |
|---|---|
| Ruleta europea | 2.70% |
| Ruleta americana | 5.26% |
| Ruleta francesa | 2.66% |
Recuerda
La ventaja de la casa de la ruleta francesa es ligeramente menor que la de la ruleta europea, pero solo si se colocan apuestas de dinero par.
Conclusión
La ruleta es un juego cuyos aspectos matemáticos básicos son fáciles de entender y memorizar. Recomiendo revisar las guías de la Academia de la ruleta para familiarizarse con lo básico.
Las probabilidades de ganar en la ruleta asociadas con cualquier apuesta se calculan como la relación entre la longitud de la cobertura de esa apuesta (cuántos números cubre la apuesta) y el número total de números en la rueda (37 o 38).
La ventaja de la casa de la ruleta solo puede tomar tres valores, dependiendo de la versión. La ventaja de la casa es fija y no puede reducirse jugando estrategias óptimas.
La mejor estrategia de apuestas disponible para la ruleta es aumentar la cobertura general de las apuestas estáticas o jugar sistemas progresivos.
Para la primera, aumentar las probabilidades de ganar se hace a costa de reducir la tasa de ganancia en caso de una victoria. Para la segunda, el mismo principio se aplica y, además, el saldo es esencial.
En la ruleta, como en otros juegos de azar, hay un equilibrio entre probabilidades de ganar, tasa de ganancia y expectativa, y ninguna estrategia objetiva puede tener en cuenta solo un factor u otro, sino todos juntos.






