Las matemáticas detrás de las probabilidades de las tragamonedas: la perspectiva de un matemático

Las probabilidades de las tragamonedas son un tema de gran controversia. Exploremos el diseño, la diversidad, la privacidad, la brevedad y el atractivo de las grandes ganancias de este juego.

En esta guía, el Prof. Catalin Baroianu, PhD, cubrirá los conceptos matemáticos y de diseño detrás de las máquinas tragamonedas de manera simple y concisa.

Esto es lo que aprenderás:

• ¿Qué son las probabilidades de las tragamonedas y por qué importan?
• El diseño y la configuración de un juego de tragamonedas
• Explicación de las hojas de Informe de cuentas de probabilidad (PAR)
• Generadores de números aleatorios (RNG) en tragamonedas
• Ventaja de la casa y RTP en tragamonedas
• Conceptos básicos de matemáticas de tragamonedas en jerga de tragamonedas
• Volatilidad en tragamonedas
• Casi-ganancias artificiales en tragamonedas
• Tragamonedas con jackpot progresivo: ¿Cuál es la matemática detrás de ellas?
• Criterios objetivos para elegir un juego de tragamonedas
• Mitos y realidades sobre las tragamonedas

Empecemos.

¿Qué son las probabilidades de las tragamonedas y por qué importan?

Las tragamonedas son un juego de extremos: Los jackpots más altos en la historia del juego – en el orden de decenas de millones – se han ganado en tragamonedas (progresivas).

Las tragamonedas son el único juego de casino cuya configuración interna y diseño son mantenidos en secreto por sus productores.

Las tragamonedas son reconocidas por expertos en juego problemático como el juego de azar que conlleva el mayor riesgo de desarrollar un comportamiento adictivo al juego.

Con tales características, el juego de las tragamonedas tiene un estatus especial entre los juegos de casino y por esto los jugadores de tragamonedas deben informarse sobre los aspectos internos de las tragamonedas como primer requisito para un juego responsable y seguro.

El diseño y la configuración de un juego de tragamonedas

Cuando estamos frente a una máquina tragamonedas y disfrutamos de su interfaz, vemos una línea o cuadrícula de espacios donde se muestra el resultado del juego después de una tirada como combinaciones de símbolos.

Esto es lo que llamamos la ventana de símbolos.

Además, hay una ventana de pago donde se definen las combinaciones ganadoras y se asigna una tasa de pago a cada una (también llamada la tabla de pagos).

Estos son los dos componentes principales de una máquina tragamonedas que comparten información sobre el juego: la primera se refiere a lo que obtienes como resultado y la segunda a cuánto obtienes como premio.

La interfaz de la máquina tragamonedas

La interfaz de la tragamonedas te muestra las reglas del juego, sin embargo, para estar completamente informado sobre el juego que juegas, también debes saber qué hay detrás de esa interfaz, es decir, cómo está configurado el juego.

Cada espacio en la línea o cuadrícula en la ventana de símbolos está asociado con uno o más carretes, que pueden ser físicos o virtuales.

El carrete consiste en un número de paradas, a las que se asignan símbolos, según el diseño particular de esa máquina.

No puedes ver un carrete completo en la interfaz (a menos que retires la carcasa de la máquina, en las tragamonedas mecánicas o electromecánicas antiguas), sino solo esa parada que es visible en el espacio de la ventana de símbolos asociada a ese carrete.

Después de la tirada, el resultado consiste en la combinación de símbolos mostrados en la ventana de símbolos y está determinado por las paradas que fueron seleccionadas (una por carrete) aleatoriamente por el RNG o los procesos mecánicos de giro, en tragamonedas (electro)mecánicas.

Entendiendo los carretes de las tragamonedas

Los carretes físicos clásicos de las antiguas máquinas tragamonedas inicialmente tenían 22 paradas y este es el número promedio de paradas que un carrete físico puede contener, incluyendo las tragamonedas de segunda generación (electromecánicas).

Sin embargo, los productores de tragamonedas querían tener más y más paradas en los carretes (para la diversidad de las combinaciones de símbolos, pero principalmente por razones relacionadas con el beneficio estadístico).

Con la evolución tecnológica de las tragamonedas, los carretes virtuales se convirtieron en el componente principal de una máquina tragamonedas.

La mayor ventaja para el productor fue que el carrete virtual puede tener paradas en cualquier número.

Los carretes virtuales reemplazaron a los carretes físicos para la tercera generación de tragamonedas (video tragamonedas), pero estos últimos no fueron abandonados por completo y en las tragamonedas electromecánicas contemporáneas trabajan junto con los carretes virtuales.

Solo podemos ver los carretes físicos en la interfaz; sin embargo, el resultado está determinado en los carretes virtuales invisibles:

1. El carrete físico está diseñado de tal manera que puede contener símbolos en cierto número de instancias (posiblemente solo una instancia de cada uno, para contener tantos como sea posible);
2. Cada uno de estos símbolos se asignan a un mayor número de instancias en el carrete virtual;
3. Luego, el carrete virtual se mapea en el carrete físico (varias paradas con el mismo símbolo en el carrete virtual se mapean en una parada en el carrete físico que contiene el mismo símbolo).
4. El RNG selecciona aleatoriamente una parada en el carrete virtual, lo que ordena al carrete físico que se detenga en la parada física mapeada.

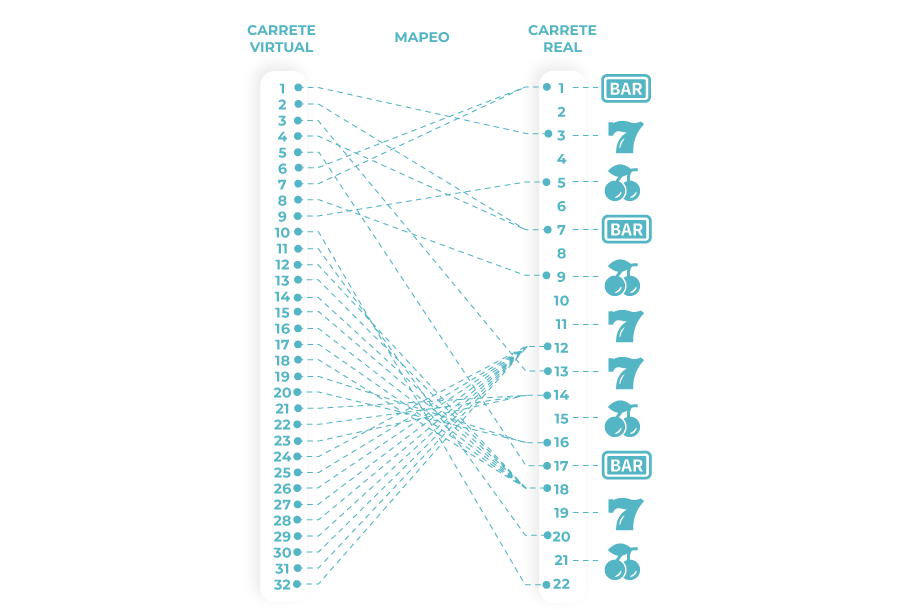
Desde esta descripción de cómo funciona una máquina tragamonedas, se puede ver claramente cuáles son los parámetros que caracterizan la configuración interna de un juego de tragamonedas:

• El número de símbolos distintos (p); símbolos denotados (por ejemplo, cereza, barra, siete, etc.);

 

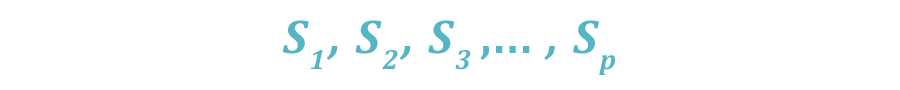
• El número de carretes (n);
• El número de paradas en cada carrete:

• Para cada símbolo S, el número de instancias de S en cada uno de los carretes

• es el número de instancias del símbolo

• en el carrete n.º j; 1 ≤ i ≤ p, 1 ≤ j ≤ n)

La matriz se llama la distribución de los símbolos en los carretes, comúnmente llamada el peso de los carretes. Los símbolos se distribuyen en cada carrete en un cierto peso y disposición.

Cada instancia de los parámetros anteriores proporciona una configuración particular y un juego de tragamonedas distinto.

Estos parámetros son los datos necesarios para cualquier cálculo de probabilidad y estadística sobre un juego de tragamonedas en particular, incluidas las probabilidades de obtener una combinación específica que paga, los valores esperados y la ventaja de la casa.

En ausencia de estos datos para un juego en particular, solo podemos proporcionar fórmulas de probabilidad general con los parámetros como variables.

Explicación de las hojas de informe de cuentas de probabilidad (PAR)

Los parámetros que determinan la configuración interna de un juego de tragamonedas y algunos resultados estadísticos básicos se anotan en la llamada hoja PAR (Probability Account Report / Informe de la cuenta de probabilidad) de ese juego.

Una hoja PAR consiste en tablas de valores.

Una tabla anota el peso de los carretes, es decir, cuántos símbolos de cada tipo hay en cada carrete. El ejemplo a continuación es de la hoja PAR del juego de tragamonedas de tres carretes "In the Money" de Bally:

Símbolos		R1	R2	R3
R7	Siete rojo	1	1	1
G7	Siete dorado	6	6	4
5X	Bar de cinco	3	1	1
MU	Función In The Money	12	12	11
MB	Espacio especial In The Money	6	6	6
3B	Bar Triple	8	7	5
2B	Bar Doble	8	9	8
1B	Bar Simple	8	11	8
CH	Cereza	2	2	2
BL	Espacio	18	17	26
Total		72	72	72
Total de combinaciones		373248

Peso de símbolos en una hoja PAR.

• Los 10 símbolos distintos del juego están anotados en las dos primeras columnas (p = 10).
• Las columnas R1, R2 y R3 contienen el peso de cada carrete, es decir, cuántas instancias de cada símbolo hay en cada carrete (parámetros en nuestra notación, i de 1 a p).
• El total de estas instancias en cada carrete (72) representa el número de paradas de cada carrete.
• El valor que aparece en la fila 'Total de combinaciones' es el número de todas las posibles combinaciones de paradas (no de símbolos distintos) que pueden ocurrir como resultado. Ese número se obtiene por multiplicación: 72 x 72 x 72 = 373,248.
• Solo una parte de todas estas combinaciones posibles son ganadoras y se pagan según las reglas de pago del juego.

Las combinaciones ganadoras de símbolos se muestran en la ventana de pago de la interfaz y la hoja PAR también las anota en una tabla junto con el número de combinaciones de paradas que las producen y sus tasas de pago asociadas:

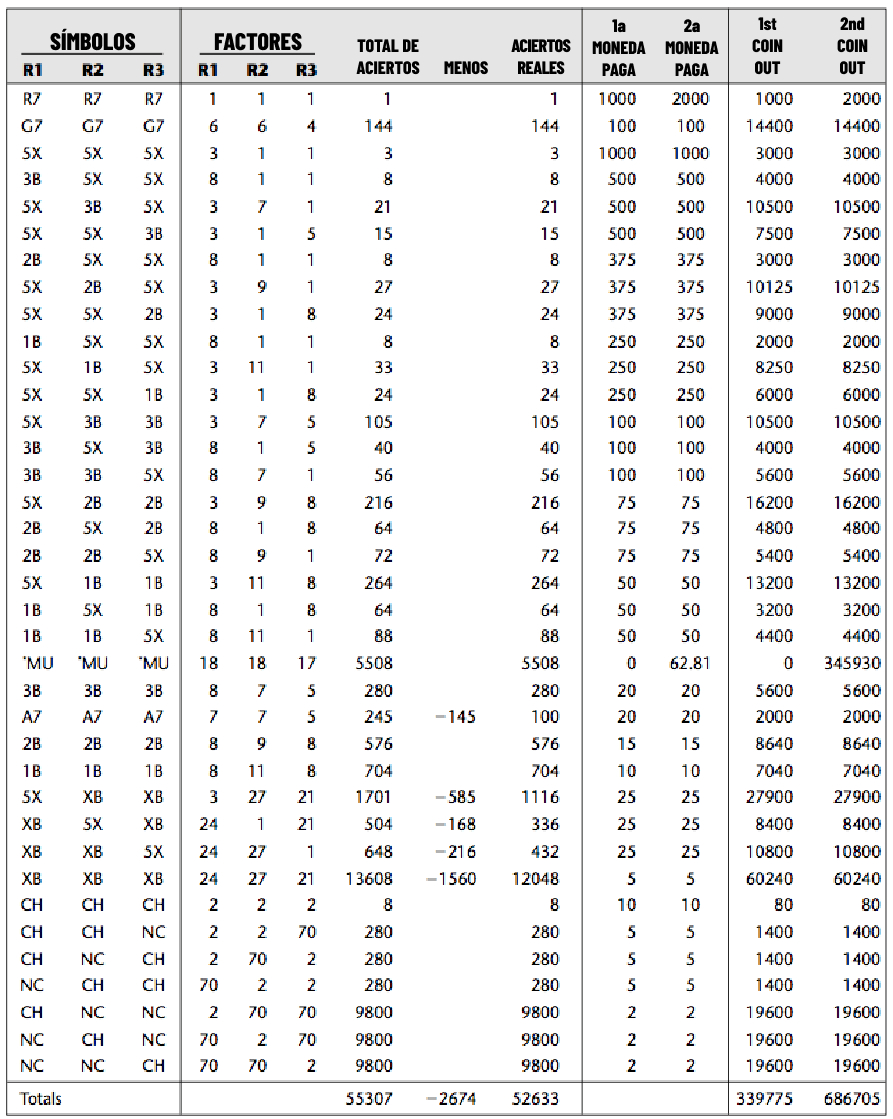
Explicación de la tabla

En la primera columna se anotan las combinaciones ganadoras de símbolos (en las denominaciones de la primera tabla), donde:

• XB denota ‘Cualquier Bar’ (3B, 2B o 1B);
• A7 denota ‘Cualquier Siete’ (A7 o G7);
• NC denota ‘Cualquier símbolo o espacio excepto una cereza’;
• * indica un pago disperso.

La columna etiquetada como 'Factores' anota para cada combinación ganadora el número de instancias de esos símbolos en cada carrete (como paradas). La columna etiquetada como 

'Total de aciertos' anota el número de combinaciones de esas paradas particulares, que representa el producto de los tres factores en esa línea.

Los valores en la columna etiquetada como 'aciertos reales' corrigen los valores de 'Total de aciertos' para esas combinaciones que contienen los elementos múltiples ‘Cualquier Bar’ o ‘Cualquier Siete’, para que cada combinación de paradas se cuente solo una vez.

La columna etiquetada como 'Pago por la primera moneda' anota el pago por cada combinación ganadora, por un crédito apostado.

La columna etiquetada como 'Pago por la segunda moneda' anota el pago por dos créditos apostados.

La última columna anota el pago total de la máquina por cada combinación ganadora, asumiendo que ocurrieron todos los aciertos.

Por qué es importante la hoja PAR

Con estos datos disponibles, uno puede fácilmente calcular la frecuencia promedio de una combinación ganadora como la relación de los valores de golpes reales / total de combinaciones, que es la probabilidad de esa combinación.

La hoja PAR también anota datos estadísticos, como la frecuencia de golpes, frecuencia de pago, porcentaje de pago de la máquina (RTP) y su índice de volatilidad, nociones de las que hablaremos en la siguiente sección.

Los últimos métodos suponen el registro de la frecuencia relativa de cada símbolo en cada carrete durante un número extremadamente largo de giros (en el orden de decenas de miles o más).

Luego, el número aproximado de paradas y el peso de los carretes se determinan mediante técnicas numéricas de aproximación.

Una vez que se recupera esta configuración paramétrica, se pueden calcular todas las probabilidades e indicadores estadísticos de un juego de tragamonedas.

Expertos e investigadores han recuperado a lo largo del tiempo las hojas PAR de muchos juegos de tragamonedas, que están disponibles gratuitamente en internet o en publicaciones relacionadas con juegos.

Líneas de pago y probabilidades de pago

La ventana de símbolos de una máquina tragamonedas consiste en una cuadrícula de espacios de símbolos, donde una o más líneas están marcadas como 'líneas de pago'.

Una línea es un camino que conecta tres o más espacios y el número de espacios conectados se llama la longitud de esa línea.

Uno o más espacios corresponden a un carrete.

En las tragamonedas de video, un carrete virtual puede mostrar varios espacios, mientras que en las tragamonedas de cuadrícula de gran tamaño, generalmente un espacio corresponde a un carrete.

La ventana de símbolos muestra el resultado del juego después del giro y las líneas de pago representan esa parte del resultado que determina si es ganador o perdedor.

Dependiendo del juego, un jugador puede habilitar una o más líneas de pago para un giro. Para que un resultado sea ganador, es necesario que la combinación de símbolos que aparezca en una línea de pago habilitada coincida con una de las combinaciones ganadoras definidas en la ventana de pago.

Para la primera generación de tragamonedas, incluidas las tragamonedas mecánicas, la ventana de símbolos consistía en una sola línea, que también era la única línea de pago, generalmente con tres o cinco espacios.

Con la evolución de las máquinas tragamonedas, la cuadrícula de la ventana de símbolos aumentó en tamaño y también el número de líneas de pago, que pueden tener varias formas y orientaciones:

• horizontal;
• vertical;
• oblicua;
• transversal;
• simétrica;
• triangular;
• trapezoidal;
• zigzag.

Ejemplos de líneas de pago

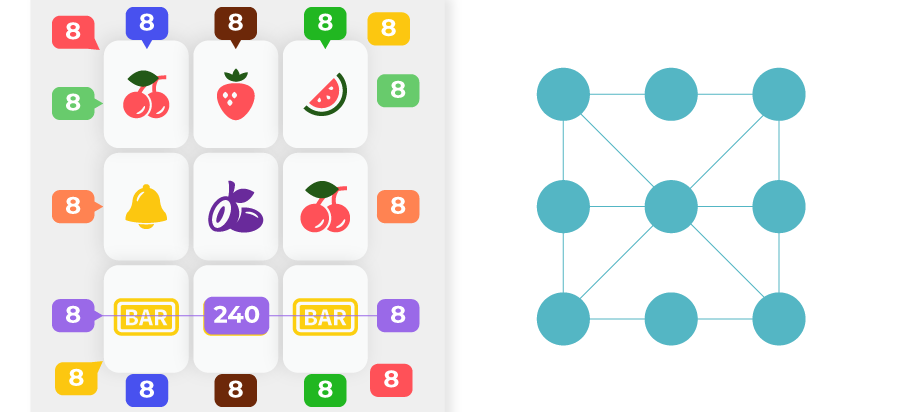
Ventana de símbolos de una máquina tragamonedas de 9 carretes con 8 líneas de pago de longitud 3 (horizontal, vertical y oblicua, todas transversales), representada como una cuadrícula de 3 x 3 espacios. Cada espacio corresponde a un carrete

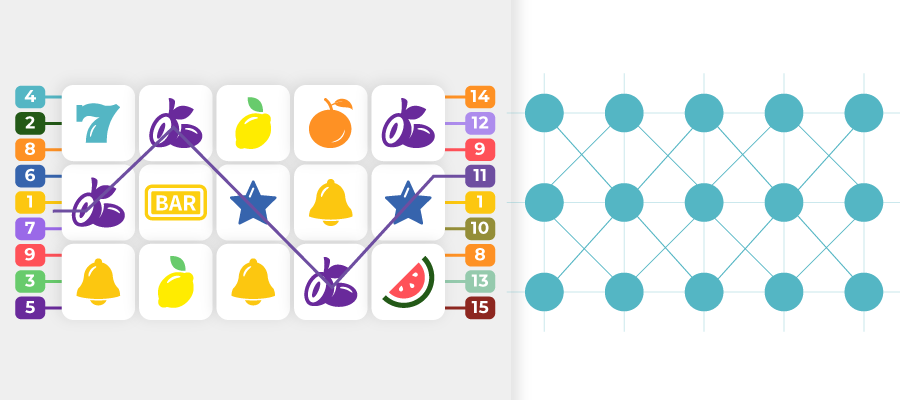
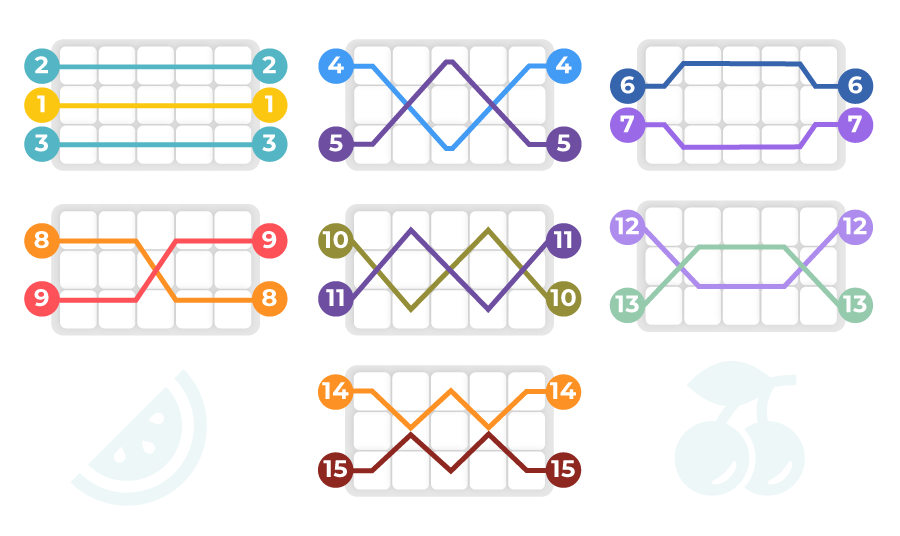
Ventana de símbolos de una máquina tragamonedas de 5 carretes con 15 líneas de pago transversales de longitud 5 (horizontal, triangular, simétrica, trapezoidal, zigzag), representada como una cuadrícula de 3 x 5 espacios.

Cada tres espacios adyacentes como una línea vertical corresponden a un carrete.

¿Por qué son importantes las líneas de pago?

La complejidad de las líneas de pago cuenta tanto como la diversidad y el diseño, características que hacen que el juego sea atractivo.

Desde el punto de vista del productor, sólo cuenta su longitud.

Sea cual sea la forma o longitud de las líneas de pago, la mayoría de ellas están diseñadas para cruzar completamente los carretes, es decir, conectando puntos correspondientes uno a cada carrete.

Como tal, el resultado en una línea de pago estará determinado por una parada de cada carrete y, dado que los carretes giran de manera independiente, las estadísticas asociadas con ese resultado solo emplearán la longitud de la línea de pago y el peso de los símbolos de cada carrete.

Entender las probabilidades de pago en las tragamonedas

Cada combinación ganadora que ocurre en una línea de pago tiene sus probabilidades de pago asignadas en el diseño del juego.

Estas probabilidades de pago se muestran en la ventana de pagos de la máquina en formato de probabilidades (por ejemplo, 50 : 1, o ‘50 a 1’), coeficiente de multiplicación (por ejemplo, x50) o cantidad de pago relativa al crédito (por ejemplo, 50, correspondiente a un crédito/moneda, y 100, correspondiente a dos créditos/monedas).

La tabla que contiene las probabilidades de pago también se llama la tabla de pagos de esa máquina.

La característica común de las tablas de pagos en los juegos de tragamonedas es que invierten el orden de las probabilidades.

Las probabilidades de pago son aproximadamente inversamente proporcionales a las probabilidades: cuanto mayor es la probabilidad de una combinación ganadora, menores son sus probabilidades de pago.

Tomemos como ejemplo concreto las probabilidades de pago del juego In the Money en nuestro ejemplo de hoja PAR.

Vamos a tomar un ejemplo. Consideramos solo las combinaciones ganadoras (R7 R7 R7), (3B 5X 5X), (5X 1B 5X) y (1B 1B 1B). Sus probabilidades de pago y probabilidades se anotan en la siguiente tabla:

COMBINACIÓN GANADORA	PROBABILIDADES DE PAGO (POR 1 MONEDA)	PROBABILIDAD
R7 R7 R7	1000	0.000002679 o 1/373,248
3B 5X 5X	500	0.000021432 o 1/46,656
5X 1B 5X	250	0.000088407 o 1/11,311
1B 1B 1B	10	0.001886016 o 1/530

En el ejemplo anterior puede notar que el orden de los pagos está invertido para las probabilidades.

Además, las probabilidades de pago no se acercan ni remotamente a la frecuencia relativa expresada por su probabilidad.

Uno puede percibir eso con razón como un despojo de dinero.

De hecho, si obtiene esa combinación una vez cada 530 giros, hay alrededor de 529 giros no ganadores y la máquina le devuelve solo 10 de los 529 créditos perdidos (¡aproximadamente 53 veces menos que su pérdida)!

Esta es una característica común de todos los juegos de tragamonedas: las probabilidades de pago no reflejan las verdaderas probabilidades. Además, la diferencia entre ellas puede variar en cualquier rango entre los diferentes juegos.

De hecho, es esa diferencia entre las dos probabilidades lo que da la ventaja al casino y al productor.

Además, las probabilidades de pago no pueden tomarse como indicio o información sobre las probabilidades de las combinaciones ganadoras, ya que las primeras pueden ser cientos o miles de veces superiores a las últimas.

Por supuesto, hay cuestiones éticas con esa diferencia, aún más cuando no se conocen las verdaderas probabilidades ya que se mantienen en secreto, sin embargo, no hay ninguna legislación en ninguna jurisdicción que regule este indicador.

Desde un punto de vista matemático, existe un indicador que mide este tipo de “equidad”, del cual hablaremos en una sección posterior.

Generadores de números aleatorios (RNG) en tragamonedas

Un generador de números aleatorios (RNG) es un dispositivo físico o electrónico o software por el cual se pueden generar números aleatorios dentro de un cierto rango o conjunto.

Aquí, ‘aleatoriamente’ significa que cualquier resultado es independiente del resultado anterior y los números están lo más uniformemente distribuidos posible en la secuencia obtenida.

Los generadores de números aleatorios basados en software también se llaman generadores de números pseudoaleatorios (PRNG) y funcionan sobre la base de algoritmos que explotan propiedades matemáticas específicas de algunas funciones.

En las tragamonedas mecánicas antiguas y en algunas tragamonedas electromecánicas, el resultado se determinaba mecánicamente, como resultado de activar el mecanismo que hace girar los carretes.

Dichos mecanismos tienen características físicas que proporcionan una aleatoriedad aceptable para los resultados de los giros: una velocidad de rotación suficientemente alta para cada carrete, los carretes giran de manera independiente en algún momento y los giros de los carretes están desfasados entre sí.

Es como en la ruleta girada por un crupier, donde todos aceptan que el giro es aleatorio.

Las tragamonedas de carrete virtual y las tragamonedas electromecánicas con carretes virtuales mapeados necesitan en su lugar un PRNG.

Cómo funciona el PRNG

Cada parada en un carrete virtual tiene un número asociado.

El PRNG funciona para cada carrete por separado y genera números aleatorios del 1 al número de paradas en ese carrete. La máquina ordena a los carretes que dejen de girar en las paradas seleccionadas por el PRNG en los puntos mostrados.

Como tal, el PRNG no selecciona símbolos en un carrete, sino paradas (que contienen símbolos). Un espacio en un carrete también es un símbolo y cuando la máquina muestra un espacio, el PRNG realmente selecciona un espacio específico (es decir, la parada específica que contiene ese espacio).

El PRNG funciona de forma continua, incluso cuando no está jugando, eligiendo cientos o miles de números por segundo. Por lo tanto, el resultado se determina antes de ser mostrado y no es el resultado de ningún comando físico del jugador (presionar el botón de giro o detener o tirar de la palanca).

El PRNG garantiza la hipótesis de que cualquier combinación de paradas de los carretes (no de símbolos) tiene la misma probabilidad de ocurrencia como resultado (precisamente, una en el producto entre el número de paradas en cada carrete).

El hecho de que algunas combinaciones de símbolos o símbolos ocurran con más frecuencia que otras está relacionado con el peso de los símbolos de los carretes.

Para el sistema de jackpot "debe ganar antes de", el PRNG generalmente funciona de la siguiente manera: genera un número aleatorio dentro de todo el rango del monto del jackpot (valor mínimo a máximo, ya sea en números enteros o decimales) o dentro de un intervalo elegido incluido en este rango, como el punto de activación.

Para el sistema de jackpot ilimitado, el PRNG puede generar números asociados con intervalos de tiempo, valores del medidor, máquinas, montos de apuestas, etc.

El algoritmo específico del sistema combina estas entradas para determinar cuándo se ganará el jackpot; sin embargo, tales algoritmos varían de un sistema a otro y no son conocidos ni predecibles.

Para más detalles sobre cómo funciona un RNG, consulte nuestra guía de RNG.

Probabilidades en tragamonedas

En las tragamonedas podemos hablar de la probabilidad de los eventos relacionados con las combinaciones ganadoras mostradas en la ventana de pagos.

Sin embargo, podemos estimarlas o calcularlas con precisión solo si tenemos la hoja PAR del juego respectivo o hemos recuperado su configuración paramétrica mediante métodos estadísticos basados en seguimiento.

Dichos eventos ganadores pueden ser:

• una combinación ganadora en particular
• una de varias combinaciones ganadoras dadas
• cualquier combinación ganadora, en una o varias líneas de pago.

El cálculo de la probabilidad de cualquiera de estos eventos utiliza una fórmula general en forma combinatoria:

La probabilidad de que ocurra un evento E en una línea de pago de longitud n (que cruza n carretes) es:

donde F(E) es el número de combinaciones de paradas en esa línea de pago favorables para que ocurra el evento E, y los ts indexados denotan el número de paradas de cada carrete cruzado por esa línea de pago.

F(E) depende de los otros parámetros del juego además del número de paradas en cada carrete (los ts) y n, a saber p y =

(explicados en la primera sección). F(E) se calcula utilizando fórmulas combinatorias más o menos complejas, dependiendo del evento en cuestión.

Para combinaciones que involucran dos o más símbolos en la línea de pago, el conteo combinatorio se complica más.

La relación entre las probabilidades de pago y la probabilidad

Como sabemos ahora, las probabilidades de las diversas combinaciones ganadoras o la probabilidad de cualquier evento relacionado con el resultado en las tragamonedas no pueden calcularse numéricamente a menos que conozcamos de antemano la configuración paramétrica de ese juego.

Las probabilidades de pago tampoco nos dan ninguna pista sobre esas probabilidades. Sin embargo, solo podemos suponer que estas probabilidades son muy bajas, y los ejemplos anteriores, imaginarios o reales, confirman eso.

Cuanto mayor sea el número de paradas en un carrete y más carretes haya, menores serán las probabilidades de obtener las combinaciones ganadoras.

En particular, se supone que la probabilidad de la combinación del jackpot (el jackpot regular) es "astronómicamente baja" y, para algunos juegos, su orden puede compararse con el orden de las probabilidades de ganar el jackpot de la lotería (uno en millones o en decenas de millones).

Solo para fines ilustrativos y no asociados con ningún juego de tragamonedas real en particular, anoté en la siguiente tabla algunos valores numéricos para esta probabilidad, bajo los siguientes supuestos: el símbolo del premio mayor tiene sólo una instancia en cada carrete y los carretes tienen el mismo número de paradas.

Por supuesto, esas probabilidades del orden de 1 en miles de millones no están realmente asociadas con juegos existentes, ya que el símbolo del premio mayor generalmente tiene más peso a medida que aumenta el número de carretes y sus paradas.

La idea es que las probabilidades de ganar las combinaciones del premio mayor pueden ser de cualquier orden y se supone que el resto de las combinaciones ganadoras también tienen bajas probabilidades. En un ranking de los juegos de azar con las probabilidades de ganar más bajas, las tragamonedas comparten el último lugar con la lotería.

Equidad de un juego de tragamonedas

¿Qué significa que un juego de azar o una apuesta sea justa?

Matemáticamente hablando, una apuesta es justa sólo si su valor esperado es cero, sin embargo, no verá una apuesta así disponible en un casino, ya que un valor esperado de cero significa cero ventaja para la casa y la casa no obtendría ganancias de dicha apuesta a largo plazo.

Por otro lado, una apuesta es un producto comercial como cualquier otro, por lo que tener una ventaja para la casa en forma de un margen comercial parece lo suficientemente justo para que ese producto permanezca en el mercado de juegos de azar.

Una ventaja positiva para la casa (que asegura la ganancia de la casa) para una apuesta es el resultado directo de tener las probabilidades de pago más bajas que las probabilidades reales (o la inversa de la tasa de pago mayor que la probabilidad de ese evento ganador).

La ventaja de la casa puede tomarse como una medida de la equidad promedio de un juego, pero cada apuesta o premio en particular puede tener su propia equidad y esto debería preocupar a los jugadores que persiguen o apuntan a premios específicos en un juego.

Esto también se aplica a las tragamonedas, donde cada jugador apunta a un premio mayor o a un premio de menor rango.

Vimos en una sección anterior cómo las probabilidades de pago difieren de las probabilidades reales de las combinaciones ganadoras y la magnitud de esa diferencia refleja una medida de un tipo de equidad de esos pagos.

En las matemáticas del juego, hay una noción que describe la equidad de una apuesta o de un premio de tragamonedas.

Ahora, apliquemos esta noción a un juego de tragamonedas real, concretamente Blazing 7s de Quick Casino Slots.

Ejemplo de cálculo de la equidad de una tragamonedas

Consideremos tres combinaciones ganadoras en Blazing 7s.

La combinación ganadora del premio mayor es Blazing 7 (B7) - Blazing 7 (B7) - Double jackpot (DJ);
La segunda combinación en el ranking de la tabla de pagos es Blazing 7 (B7) - Blazing 7 (B7) - Blazing 7 (B7);
Una combinación de rango medio es Double bar (2B) - Double bar (2B) - Double bar (2B).

Según la tabla de pagos y la hoja PAR del juego, las siguientes tasas de pago y probabilidades están asociadas a estas combinaciones:

COMBINACIÓN GANADORA	TASA DE PAGO (PARA LA 2DA MONEDA)	PROBABILIDAD
B7 B7 DJ	x2500	0.00001071
B7 B7 B7	x500	0.00024648
2B 2B 2B	x40	0.00194508

Ahora calculemos la equidad matemática para cada premio:

• Para (B7 B7 DJ), la equidad matemática es f = 2,500×0.00001071 / (1 – 0.00001071) = 0.0267 o 2.67%.
• Para (B7 B7 B7), la equidad matemática es f = 500×0.00024648 / (1 – 0.00024648) = 0.1232 o 12.32%.
• Para (2B 2B 2B), la equidad matemática es f = 40×0.00194508 / (1 – 0.00194508) = 0.0776 o 7.76%.

Con estas cifras, la tasa de pago de ×2,500 para la combinación ganadora del premio mayor en nuestro ejemplo ya no parece una oferta tan generosa, ¿verdad?

Si bien agregar un margen comercial al costo de un producto es una elección económica justa, no tener ese margen transparente para los clientes ya no es una práctica comercial justa, especialmente cuando ese margen es mucho mayor que para productos de la misma categoría.

En las tragamonedas, el margen es desconocido ya que no tenemos acceso a todos los parámetros del juego.

La equidad matemática de una apuesta, suponiendo que sea conocida o calculable, puede ser un criterio para elegir un juego u otro, al igual que otros indicadores estadísticos de un juego.

Ventaja de la casa y RTP en las tragamonedas

Al jugar en las tragamonedas, realizas una apuesta como en cualquier otro juego de azar, y tu apuesta es que una combinación ganadora de símbolos aparecerá en una o más líneas de pago. Esta apuesta tiene su propio valor esperado, que depende de tu apuesta, las probabilidades de pago y las probabilidades asociadas con cada combinación ganadora, según la fórmula bien conocida:

EV = probabilidad de ganar × ganancia si ganas + probabilidad de perder × la perdida si pierdes.

El valor esperado (EV) también puede expresarse en forma de porcentaje, como relación de la apuesta inicial.

Cada juego de tragamonedas tiene una ventaja de la casa (HE, por sus siglas en inglés) definida como el inverso (en signo, menos se convierte en más) del valor esperado de una apuesta.

La HE refleja la ganancia del casino a largo plazo, como un porcentaje de todas las apuestas de los jugadores.

Generalmente, en las tragamonedas, si

son las combinaciones ganadoras,

son las probabilidades de que estas combinaciones ocurran en una línea de pago,

son sus tasas de pago respectivamente, y c es tu apuesta, entonces:

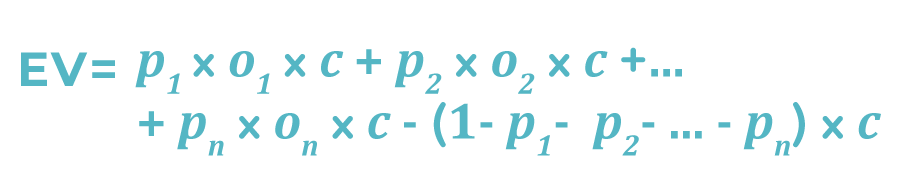
o, como una proporción de la apuesta inicial: 

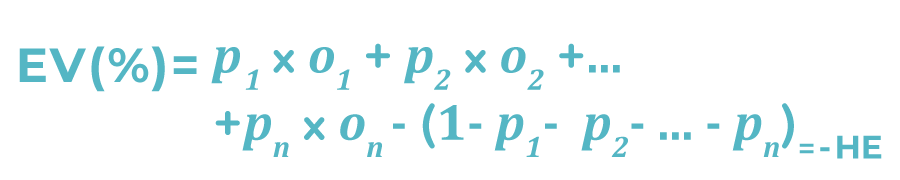
Nuevamente, los únicos parámetros de las fórmulas anteriores que podemos conocer son las probabilidades de pago Oi. Para poder calcular numéricamente el EV y el HE, deberíamos conocer las probabilidades Pi

Comprendiendo el RTP de las tragamonedas

En las tragamonedas, la ventaja de la casa generalmente se expresa no en términos de la ganancia de la casa, sino de los pagos a los jugadores. El indicador estadístico llamado Retorno al Jugador (RTP, por sus siglas en inglés), también conocido como el porcentaje de devolución, se define como:

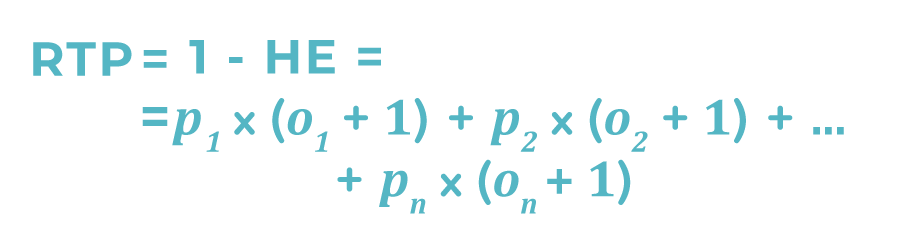
Todos los EV, HE y RTP son promedios estadísticos que indican un resultado acumulativo a largo plazo.

Matemáticamente, "a largo plazo" significa una serie infinita de giros en las mismas condiciones. En realidad, cuanto más larga sea la serie de giros, más se acercarán las ganancias o pérdidas acumuladas al valor de estos indicadores.

Dado que el RTP es un promedio estadístico, debe interpretarse como tal: El RTP es el porcentaje del total de las cantidades apostadas que una máquina devuelve a sus jugadores como premios a largo plazo.

El RTP de los juegos de tragamonedas generalmente varía entre el 80% y el 99%, pero este alto porcentaje no debe interpretarse como una ganancia o ventaja para el jugador.

Por el contrario, refleja una pérdida promedio, ya que el RTP es solo otra forma de expresar la ventaja de la casa: la ventaja de la casa es 1 – RTP, que es lo opuesto al valor esperado.

El RTP es el único indicador estadístico que se muestra en muchas máquinas tragamonedas, en su sección de ayuda/acerca de (en algunos casos raros, también muestran el índice de volatilidad).

Los productores revelan el RTP ya sea voluntariamente o porque están obligados por las regulaciones locales de juego. Sin embargo, esta información está sujeta a varias y frecuentes malas interpretaciones por parte de los jugadores.

Malas interpretaciones del RTP

El RTP es muchas veces la única información estadística disponible sobre un juego de tragamonedas y el criterio principal para elegir un juego u otro. De hecho, cuanto mayor sea la devolución de un juego, mayores serán las posibilidades de que un jugador obtenga algunos premios durante su sesión de juego.

Vimos en la sección anterior que el RTP, por su definición, es una noción matemática abstracta, estrechamente relacionada con el valor esperado.

Cuando hablamos del RTP en un contexto no matemático, es decir, el juego real, debemos tener una interpretación adecuada de la noción en sí y su aplicación.

Desafortunadamente, muchos jugadores malinterpretan el RTP y, al hacerlo, tienen una visión distorsionada de cómo funciona una máquina tragamonedas y la ganancia que deberían esperar de su juego.

Las principales malas interpretaciones del RTP junto con sus correcciones son las siguientes:

RTP como una ventaja o ganancia

Influidos por la descripción verbal de la noción y no por la matemática, algunos jugadores perciben el "retorno" como una especie de ganancia esperada que se sumará a sus ganancias. Los valores de este indicador (generalmente cercanos al 100%) a veces se perciben como ventajosos desde la perspectiva del jugador.

El RTP en realidad refleja la ventaja de la casa en términos del reembolso a los jugadores, por lo tanto, el RTP en realidad refleja una pérdida promedio y no una ganancia.

RTP aplicándose a sesiones individuales o juegos a corto plazo

Algunos jugadores piensan que el RTP puede aplicarse a su propia sesión de juego, sea cual sea su duración, es decir, que la máquina devolverá ese porcentaje de sus apuestas recolectadas desde el momento de inicio hasta que detengan la sesión.

Otros piensan que la máquina devolverá ese porcentaje acumulativamente a todos los jugadores que jueguen en esa máquina durante un día, una semana o más. El RTP es un promedio estadístico basado en la probabilidad. En el juego real (que es finito) sólo podemos referirnos al RTP como un límite al que se aproxima a largo plazo, específico de ese juego.

Por lo tanto, cualquier aplicación del RTP en intervalos definidos de juegos o jugadores individuales es inadecuada y conduce a estimaciones incorrectas.

Malas interpretaciones de los mensajes de RTP

Cuando la información del RTP se muestra en la tarjeta de presentación de una máquina, un mensaje clásico como "esta máquina tiene un promedio de devolución del 95%" puede ser malinterpretado por jugadores no informados de varias maneras, tales como:

• El 95% de los jugadores de esa máquina ganarán algunos premios;
• Esta máquina pagará un premio 19 veces de cada 20;
• Si apuestas $1 en esta máquina, tienes garantizado ganar 95 centavos.

Tales malas interpretaciones son favorecidas por la incorrecta comprensión del concepto de promedio estadístico, que es la naturaleza del RTP.

Hay máquinas tragamonedas con diferentes RTP, dependiendo del crédito.

La variación proviene de los bonos adicionales y diferentes probabilidades de pago que el juego ofrece para créditos más altos. Los mensajes de RTP de tales máquinas (notando los diferentes valores del RTP) también pueden ser malinterpretados, y la interpretación más común es "cuanto mayor sea la apuesta, mayores serán las probabilidades de ganar", lo cual es falso.

Nociones básicas de matemáticas en jerga de tragamonedas

Si la fórmula de probabilidad combinatoria y otras nociones que proporcionamos en secciones anteriores aún parecen complicadas para el lector no matemático, pueden expresarse en términos técnicos comúnmente usados en la jerga de las tragamonedas:

Ciclo 

El número de todas las posibles combinaciones de paradas que pueden ocurrir como resultados en una línea de pago en un juego de tragamonedas.

Representa el denominador de la fracción en la fórmula combinatoria, es decir, el producto del número de paradas de los carretes (los ts en esa fórmula).

Aciertos

El número de combinaciones de paradas que contienen una combinación ganadora de símbolos dada. Representa el numerador de la fracción en la fórmula de probabilidad.

En estos términos, la fórmula de probabilidad se escribe como:

• probabilidad (de una combinación ganadora dada) = aciertos/ciclo

El ciclo puede interpretarse como el número de giros en los que cada combinación de paradas ocurre solo una vez, mientras que los aciertos son el número de ocurrencias de la combinación ganadora dada durante ese ciclo.

Tasa de aciertos

La frecuencia relativa de una combinación ganadora dada a lo largo del tiempo.

• tasa de aciertos = 1/probabilidad = ciclo/aciertos

Frecuencia de aciertos

La tasa de aciertos expresada como porcentaje: frecuencia de aciertos = 100%/tasa de aciertos

Ganancia media 

El valor esperado para cada premio en el programa de pagos a largo plazo.

• ganancia media = premio × probabilidad (de ese premio)

Porcentaje de retorno al jugador (RTP)

Se define como: RTP = (ganancia media/apuesta media) × 100%

Volatilidad en las tragamonedas

La volatilidad es un término que refleja en la práctica la noción estadística de varianza.

La varianza es una medida de la desviación de los valores de la variable aleatoria respecto a la media o valor esperado como promedio de sus desviaciones cuadráticas.

Mide cómo se dispersan los datos respecto a su media. En términos de juego, la varianza da una medida de con qué frecuencia, en promedio, el juego devuelve dinero, así como cómo se distribuyen los premios.

En general, en las tragamonedas de baja volatilidad, puedes esperar ganancias más frecuentes y en cantidades menores que en las de alta volatilidad, donde puedes esperar más tiempo antes de obtener un premio.

La volatilidad depende directamente – como cualquier otro indicador estadístico – de la configuración paramétrica del juego.

Algunos productores de tragamonedas exponen el índice de volatilidad de sus juegos junto con el RTP, pero la mayoría no lo hace.

Para estos últimos, tienes que averiguar si se trata de un juego de baja, media o alta volatilidad.

Las tasas de pago pueden darte una pista sobre la categoría de volatilidad de un juego: por lo general, los juegos de tragamonedas que ofrecen altas tasas de pago para sus combinaciones de premios máximos (×5,000, ×8,000, etc.) o que tienen una gran diferencia entre la tasa de pago más baja y la más alta son juegos de alta volatilidad.

Los juegos que ofrecen bonos (giros gratis, pagos adicionales, etc.) también son probablemente de alta volatilidad.

Un método más preciso para encontrar la volatilidad de un juego es a través del seguimiento estadístico a largo plazo.

Casi-aciertos artificiales en las tragamonedas

En el juego, un casi-acierto es un resultado no ganador que difiere en uno o unos pocos elementos de uno ganador.

Es un fracaso que parece estar cerca de ser exitoso y ocurre en todos los juegos de azar.

Todo jugador ha experimentado el casi-acierto en su historial de juego.

Los expertos en problemas de juego afirman que el casi-acierto es un factor de riesgo para desarrollar un comportamiento de juego problemático.

Esto se debe a que este fenómeno va seguido de lo que llaman "el efecto del casi-acierto": una emoción combinada de frustración y esperanza ("¡Estuve tan cerca!") que alimenta la creencia de que una victoria es inminente y hay buenas posibilidades de que eso suceda si se dedica suficiente tiempo al juego.

Los casi-aciertos pueden ocurrir por pura casualidad – por ejemplo, pasarse en el blackjack con 22 puntos, o sacar un 12 en lugar de 11 en los dados, y así sucesivamente.

Pero también hay casi-aciertos donde la casualidad no es el único factor que determina su ocurrencia y su efecto.

Los casi-aciertos artificiales ocurren en las tragamonedas y tales hechos son el resultado del diseño interno de los juegos.

Por la naturaleza de las tragamonedas, los parámetros del juego pueden manipularse en la fase de diseño para dar como resultado resultados frecuentes que parecen casi-aciertos e interpretados por los jugadores como casi-aciertos de azar.

El casi-acierto clásico en las tragamonedas es cuando falta un símbolo en una línea de pago para tener una combinación ganadora.

Sin embargo, para los juegos que muestran cuadrículas de lugares en su ventana de símbolos, el casi-acierto y el efecto de casi-acierto también pueden estar relacionados con elementos fuera del resultado real en la línea de pago:

Puede suceder que las instancias del símbolo faltante en una línea de pago ocurran justo debajo o encima de esa línea de pago, o a la izquierda o a la derecha de ella. Este resultado extendido se percibe como un casi-acierto.

La relación de símbolos de premio y la agrupación

El casi-acierto artificial puede diseñarse para que ocurra frecuentemente en la línea de pago, eligiendo ponderaciones específicas para cada carrete.

La técnica para crear casi-aciertos artificiales adyacentes a la línea de pago se llama agrupación y se basa en la flexibilidad de la ponderación y disposición de los símbolos en los carretes virtuales.

La idea básica es colocar una parada con un símbolo de premio alto en el carrete virtual entre varias paradas con símbolos de premio bajo o espacios en blanco, mapeados en las posiciones correspondientes en el carrete físico o el carrete virtual visible en la ventana de símbolos.

Con la técnica de agrupación, las probabilidades reales de que el RNG elija un cierto símbolo en el carrete visible son diferentes a las probabilidades dadas por la ponderación real de ese símbolo en ese carrete.

De hecho, los premios bajos inmediatamente arriba y abajo del símbolo de premio alto son favorecidos en el carrete físico.

Obtener estos símbolos da a los jugadores la ilusión de que casi golpearon el símbolo de premio alto, porque ese símbolo está físicamente cerca de la línea de pago.

Pero no está matemáticamente cerca – cualquier combinación de paradas (en los carretes virtuales) tiene la misma probabilidad de ocurrencia y no cualquier combinación de símbolos.

Así, un casi-acierto artificial es solo un fallo y no tiene nada especial excepto el esfuerzo de diseño gastado para crear esa ilusión.

"Estuve tan cerca" es en realidad "Estuve tan lejos como con cualquier otra combinación perdedora", donde "lejos" debería medirse en probabilidad y no en el número de símbolos faltantes para un premio.

Tragamonedas de jackpot progresivo: ¿Cuál es la matemática detrás de ellas?

Un jackpot progresivo es un tipo de premio que se acumula con el tiempo, aumentando con cada nuevo giro, y se libera como un único premio al ganador, según las reglas vigentes para ese sistema y casino.

En la mayoría de los sistemas progresivos, hay requisitos de elegibilidad para que un jugador sea premiado con el jackpot progresivo – generalmente se requiere que consigan el premio mayor del juego (el jackpot regular) o en algunos casos cualquier premio; la mayoría de los sistemas requieren que los jugadores coloquen apuestas de un cierto tamaño para ser elegibles.

Hay 3 categorías principales de tragamonedas progresivas:

1. Progresivos independientes – máquinas tragamonedas individuales (físicas o virtuales) que acumulan fondos para el jackpot progresivo solo a partir de sus propias apuestas.
2. Progresivos locales – una red de 10 a 100 máquinas físicas en un casino, donde cada jugador en cualquier máquina de la red participa en el fondo del jackpot.
3. Progresivos de red de área amplia – una red de máquinas (físicas o virtuales) en varios casinos, en línea o físicos, funcionando en diferentes lugares, posiblemente en todo el mundo.

Cada sistema de jackpot progresivo tiene sus propias características y reglas.

En todos los sistemas, el jackpot comienza a acumularse con la primera apuesta colocada en una máquina (individual o en red) después de que el jackpot anterior ha sido liberado, y estará disponible para una nueva liberación solo después de que el monto del jackpot alcance un cierto umbral, llamado el "seed".

El valor actual del jackpot se llama "medidor de jackpot" y se muestra en todas las máquinas de la red.

La contribución al fondo del jackpot puede ser por apuesta o por ganancia y se establece como un porcentaje de las apuestas o ganancias que se dirige hacia el jackpot.

La contribución por apuesta hace que el medidor aumente con cada nuevo giro, mientras que la contribución por ganancia hace que aumente con cada nueva ganancia.

Hay dos tipos de sistemas progresivos con respecto a la liberación del jackpot:

• Debe ser ganado antes;
• Ilimitado.

El jackpot que "debe ser ganado antes" (también llamado jackpot misterioso) tiene un valor máximo asociado y puede liberarse en cualquier momento entre el "seed" y ese valor máximo.

El punto de liberación se determina aleatoriamente por el RNG después de cada reinicio del medidor y el ganador será aquel jugador cuya contribución al fondo del jackpot haga que ese valor de liberación se cumpla o se exceda.

El sistema progresivo ilimitado no tiene un límite superior para el jackpot y podría ganarse en cualquier momento después de que se pase el "seed", si se cumplen los requisitos de elegibilidad.

Es por eso que el medidor de tales sistemas puede llegar a alcanzar cantidades del orden de millones y decenas de millones, para los progresivos de red de área amplia.

Además de los parámetros de las máquinas tragamonedas individuales en una red progresiva, la propia red tiene sus propios parámetros e indicadores estadísticos y la mayoría de ellos no son conocidos por el público (¡una característica popular para las tragamonedas!).

Parámetros e indicadores estadísticos de un sistema progresivo

El porcentaje de las apuestas o ganancias que se dirige al jackpot se llama tasa de incremento del medidor.

La tasa de incremento del medidor es específica de cada sistema y los valores comunes de ella son 1% o 2%, pero también hay sistemas con una tasa inferior al 1%.

La tasa de incremento del medidor r de un progresivo no se expone, pero puede recuperarse mediante seguimiento y conteo.

Para los progresivos por contribución por apuesta, debes averiguar cuánto se necesita para mover el medidor 1 centavo ya sea jugando el juego tú mismo o observando a alguien más jugar.

Si c es el crédito apostado y a es el avance del medidor, entonces la tasa de incremento del medidor es r=100 x a/c (%).

Tal método de recuperación funciona bien para un progresivo independiente, relativamente bien para un progresivo local.

Sin embargo, para un progresivo de red de área amplia podría estar sujeto a errores y aproximaciones inexactas (ya que no sabes si más de un jugador contribuyó al avance del medidor).

En cuanto a los progresivos por ganancia, el método requiere un período de observación mucho más largo.

Otro parámetro es el "seed", que también se mantiene en secreto para la mayoría de los sistemas.

El único parámetro expuesto es el valor de "debe ser ganado antes" 
?
M para el jackpot misterioso, es decir, el valor máximo posible para ese jackpot progresivo.

Vimos que el RTP de una máquina tragamonedas no progresiva se define como la ganancia media / apuesta media.

Sin embargo, en un progresivo hay el jackpot progresivo que se suma a las ganancias dadas como premios base.

No sabemos cuándo se liberará el jackpot, ni en qué cantidad.

Solo sabemos que en algún momento futuro ocurrirá la liberación. Por lo tanto, en un progresivo, el RTP real incluyendo el jackpot es más alto que el RTP regular de las máquinas en la red.

Dado que el jackpot aumenta con cada apuesta y no se sabe cuándo se restablecerá, podemos decir que el RTP de un sistema progresivo es variable.

A diferencia del RTP regular, que es constante para una máquina, el RTP progresivo debería entenderse como dependiente del medidor: expresa el porcentaje de devolución promedio a largo plazo en el momento de la estimación, bajo la suposición de que el monto del jackpot permanecería en su valor actual.

Así, el porcentaje de devolución aumenta desde el RTP regular hacia arriba, a medida que aumenta el jackpot.

Pero el RTP es un porcentaje inferior al 100%, por lo tanto, a un cierto valor del medidor, el RTP progresivo igualará el 100% y luego irá más allá de esa cifra. Este es el momento en que el valor esperado es cero y se vuelve positivo después de este momento hasta que se restablece el jackpot.

Ese momento se llama el punto de equilibrio del sistema progresivo y es un indicador estadístico importante de él, ya que es el único asociado con una estrategia de juego en las tragamonedas progresivas.

Punto de equilibrio y juego de ventaja en tragamonedas progresivas

El punto de equilibrio de un sistema progresivo ilimitado no se puede calcular, incluso si conociéramos el RTP regular, mientras no sepamos nada sobre el algoritmo de activación del jackpot.

En cambio, el punto de equilibrio se puede estimar aproximadamente para los sistemas progresivos con un límite de activación, si conocemos el RTP regular y la tasa de incremento del medidor r, asumida por apuesta y no por ganancia.

Otra suposición para hacer posible este cálculo es que el algoritmo que activa el jackpot selecciona aleatoriamente un número de una distribución uniforme de los montos en el rango del medidor.

En estas condiciones, la siguiente regla práctica nos da un valor aproximado para la cantidad en el medidor correspondiente al punto de equilibrio:

B = M x (1 - RTP + r) / (1 - RTP + 2r), donde M es el valor máximo del jackpot.

Consideraciones estratégicas para el punto de equilibrio

El punto de equilibrio tiene una importancia estratégica en los progresivos con un límite de activación.

Una expectativa positiva de una apuesta significa que si haces esa apuesta en las mismas circunstancias a largo plazo, se espera que ganes acumulativamente más de lo que perderás con esa apuesta.

En las tragamonedas progresivas, estas circunstancias que determinan un EV positivo son los momentos después de que el medidor alcanza el punto de equilibrio.

Por lo tanto, si puedes estimar el punto de equilibrio, jugar el mismo juego repetidamente solo después de ese punto es matemáticamente óptimo como estrategia. Esta estrategia para progresivos se llama juego de ventaja.

Este juego de ventaja debe entenderse correctamente en términos de efectividad: Al jugar así, no estás aumentando tu probabilidad de ganar en una tirada, ni durante toda la sesión de juego.

Solo se te garantiza una ganancia positiva cuando ganes el jackpot a largo plazo.

Es como en el blackjack, por ejemplo, cuando jugar de manera óptima no significa que vencerás al crupier en un juego en particular, sino que tendrás una ganancia positiva a largo plazo repitiendo la estrategia.

Sin embargo, el juego repetido depende de tu saldo.

Aunque una expectativa positiva garantiza una ganancia a largo plazo, tu saldo puede no soportar el juego prolongado, especialmente en tragamonedas progresivas. Perseguir un jackpot progresivo es una elección arriesgada y puede llevar a serios daños monetarios.

Sobre la probabilidad de ganar un jackpot progresivo

Como en las tragamonedas regulares, donde las probabilidades de ganar los premios no se pueden estimar debido a la falta de datos sobre la configuración paramétrica del juego, en las tragamonedas progresivas faltan los mismos datos y también cualquier información sobre el algoritmo que activa el jackpot.

Así que todo lo que podemos hacer son suposiciones sobre el orden de probabilidad de ganar un jackpot progresivo.

¿Haría alguna diferencia si la probabilidad fuera 1 en un millón o 1 en 100 millones, mientras no se pueda mejorar mucho a través de ninguna estrategia?

Lo que sabemos con certeza es que la probabilidad de ganar el jackpot progresivo es mucho menor que la probabilidad de ganar el jackpot regular (y vimos cuán baja puede ser esta última en una sección anterior).

Para que un jugador gane el jackpot progresivo deben ocurrir dos eventos independientes:

• el jugador gana el premio base (en el jackpot por ganancia)
• el algoritmo de activación elige esa ganancia para liberar el jackpot.

Una de las propiedades básicas de la probabilidad es que la probabilidad de una conjunción de eventos independientes es el producto de las probabilidades de cada evento:

P(Jp) = P(Jb) x P(R), donde P(Jp) es la probabilidad de que el jugador gane el jackpot progresivo, P(Jb) es la probabilidad de que gane el jackpot base y P(R) es la probabilidad de que el algoritmo libere el jackpot para esa ganancia.

Sabemos que la probabilidad es un número subunitario y si hacemos el producto de dos de estos números el producto será mucho menor que cada uno de los dos factores.

P(Jb) no se puede calcular para juegos cuya configuración paramétrica no se conoce, pero ya suponemos que está en el orden de 1 en decenas de miles a 1 en cientos de miles o 1 en millones o más.

Este número ya bajo (en cualquier orden) se vuelve aún más bajo cuando se multiplica por P(R). Esta última probabilidad tampoco se puede calcular, ya que no conocemos el algoritmo detrás del sistema.

Aquí hay un ejercicio de estimación de P(R) para un sistema progresivo con un límite de activación:

Supongamos que los límites del medidor son $1,001 – $5,000.

Supongamos que el algoritmo elige aleatoriamente un nivel del medidor para liberar el jackpot sobre la distribución uniforme de los enteros dentro del rango del medidor.

Tenemos 4,000 de esos números, entonces P(R) = 1/4,000. Luego, P(Jp) = P(Jb) x (1/4,000). Supongamos una probabilidad "decente" de 1 en 10,000 para el jackpot regular.

Entonces P(Jp) = (1/10,000) x (1/4,000) = 1/40,000,000.

Las probabilidades que discutimos se aplican a una sola tirada.

La probabilidad general de que el jugador gane el jackpot en varias tiradas aumenta proporcionalmente con el número de tiradas, pero a costa de reducir el saldo, que puede agotarse en algún momento.

Es similar a la lotería, donde no puedes comprar boletos en el orden de millones para aumentar tus posibilidades de ganar el jackpot.

Además, en las tragamonedas, esos millones de tiradas te costarían dinero y tiempo y el jackpot podría simplemente ir a otra persona durante tu persecución.

Criterios objetivos para elegir un juego de tragamonedas

Los jugadores pueden elegir el juego, máquina o red de tragamonedas según diversos criterios, tanto subjetivos como objetivos.

Entre los criterios subjetivos, los temas de diseño particular que se ajustan a los hobbies o preferencias de los jugadores, la diversidad en cuanto a símbolos, líneas de pago, opciones de apuesta o el historial de premios entregados, son los más comunes.

Los criterios objetivos de elección se refieren a los resultados monetarios de un juego o máquina desde una perspectiva informativa y una perspectiva estratégica, y están relacionados con los parámetros del juego e implícitamente con los hechos estadístico-matemáticos del juego.

Es indiscutible que no existe una estrategia óptima para jugar a las tragamonedas (excepto el juego de ventaja en los progresivos que deben golpear antes de un monto específico, con la reserva asociada sobre la efectividad real de dicha estrategia).

En general, la única estrategia en las tragamonedas es la de elegir: elegir un juego, una red, elegir el tamaño de tus apuestas, elegir el tiempo que pasas jugando, y también elegir no jugar.

En esta sección, enumeraré y describiré los criterios objetivos para elegir un juego o red de tragamonedas:

RTP 

Este es el primer criterio para elegir un juego de tragamonedas, si la información del RTP está disponible – cuanto mayor sea el RTP, mejor, ya que este indicador expresa el porcentaje de reembolso. Generalmente, las tragamonedas en línea tienen RTP más altos que las de los casinos físicos.

Volatilidad

Asumiendo que la volatilidad de un juego es conocida o al menos etiquetada como baja, media o alta, puede ser un criterio para elegir un juego de tragamonedas y los factores a los que este criterio está relacionado son el saldo y el límite de tiempo de juego deseado.

Para un jugador con un saldo bajo, puede ser útil comenzar con un juego de volatilidad baja para que las posibles ganancias constantes consoliden el saldo lo suficiente como para pasar luego a juegos de volatilidad media o alta en los que buscar premios mayores.

Un jugador con un saldo grande puede elegir comenzar con juegos de volatilidad media o alta, pero, por supuesto, la otra opción no está excluida.

Para un jugador que decide jugar sesiones muy largas, independientemente de su saldo, la distinción entre volatilidad baja y alta puede no ser importante al elegir.

Los jugadores que también aspiran a jackpots progresivos generalmente juegan con las apuestas más altas, ya que la mayoría de los progresivos requieren apuestas máximas para ser elegibles para el monto del jackpot progresivo.

Tal elección no se recomienda al jugar un juego de alta volatilidad sin objetivo de jackpot progresivo, especialmente con un saldo bajo.

De lo contrario, es mejor elegir máquinas con RTP alto y alta volatilidad si es posible, para sistemas progresivos donde se requiere alcanzar el jackpot regular, y con volatilidad baja a media si se requieren otros premios base más pequeños.

Probabilidades

Los jugadores que están más interesados en las probabilidades de ganar los premios en una sola tirada en lugar de RTP o volatilidad, por ejemplo, aquellos que juegan sesiones cortas a medianas, pueden tomar la probabilidad de las diversas combinaciones ganadoras como su criterio para elegir un juego.

Por supuesto, esto es posible solo si las hojas PAR o esa información particular sobre el grupo de juegos a elegir están disponibles.

Si conociéramos tales probabilidades, inmediatamente calcularíamos la equidad matemática de los premios de los juegos y se aplicaría un nuevo criterio relacionado con las probabilidades: entre dos juegos que tienen aproximadamente las mismas probabilidades asociadas con los premios, deberías elegir el más justo.

Es un criterio natural, no necesariamente por su naturaleza ética, sino simplemente porque una apuesta más justa en condiciones de igual probabilidad supone un pago mayor e implícitamente un valor esperado mayor.

En tragamonedas progresivas, elegir una mayor probabilidad de ganar significa en realidad elegir una red pequeña de progresivos para reducir tu competencia o jugar en redes locales cuando hay un número mínimo de jugadores comprometidos.

Valor esperado

Los jugadores que buscan una estrategia que optimice el valor esperado pueden elegir los sistemas progresivos que deben golpear antes de un monto específico, donde se aplica el juego de ventaja.

Tal elección también está relacionada con otros factores de juego personal, como la duración deseada de la sesión y el saldo.

Mitos y hechos sobre las tragamonedas

La alta popularidad de las tragamonedas ha convertido este juego, con el tiempo, en una fuente de mitos que circulan entre los jugadores y son creídos como verdaderos por muchos jugadores no informados.

Algunos de estos mitos se suscriben a las generalizaciones erróneas y falacias del juego y otros son específicos de las tragamonedas; ya los hemos mencionado en esta guía.

Dado que los expertos en problemas de juego encontraron que las tragamonedas son el juego de casino más adictivo, es importante conocer los principales mitos y los hechos asociados que los desacreditan:

Mito 1: Si sigues jugando la misma máquina tragamonedas, eventualmente pagará

Hecho: Físicamente hablando, es cierto.

Pero no es un pago en sí como un evento al que deberías apuntar, sino tener un beneficio general en esa sesión y esto equivale a la duración de la racha perdedora.

Cada giro desafortunado te cuesta créditos y la pérdida se acumula hasta el giro ganador. Para tener un beneficio, el pago debe exceder la pérdida acumulada y eso depende del premio que ganaste.

Por otro lado, tu saldo debe ser lo suficientemente grande como para sostener una larga racha perdedora. Esto se aplica a cualquier juego de azar.

No hay información sobre una máquina que te diga cuánto tiempo debes jugarla antes de que pague.

Todos los indicadores estadísticos de un juego de tragamonedas – si están disponibles – son promedios estadísticos y no aritméticos. Después de todo, los resultados están determinados por el RNG, que funciona al azar.

La frecuencia de las victorias está relacionada con la probabilidad de cada combinación ganadora, pero la probabilidad es, nuevamente, un promedio infinito y no puede predecir cuándo ocurrirá una victoria. Es posible, aunque improbable, que una máquina no pague durante miles de giros o más.

Mito 2: Si casi has acertado una combinación ganadora, es una señal de que ganarás pronto

Hecho: Cada combinación de paradas en los carretes tiene la misma probabilidad de ocurrir, pero las diversas combinaciones de símbolos tienen diferentes probabilidades. Además, cada giro es independiente del anterior.

Un casi-acierto es solo un fallo y no proporciona información sobre los resultados futuros.

El casi-acierto puede ocurrir por casualidad, pero también porque el peso de los símbolos y la asignación de los carretes generalmente se manipulan por diseño para producir combinaciones frecuentes que parecen casi-aciertos, para alimentar la esperanza y hacer que juegues más.

Mito 3: Se recomienda jugar de noche para tener mayores posibilidades de ganar un jackpot progresivo

Hecho: Obviamente, por la noche hay menos jugadores en una red que durante el día. Si supiéramos que el algoritmo de activación del jackpot no involucra el factor tiempo, sería cierto que las posibilidades son mayores por la noche, ya que disminuyen con el número de jugadores en la red.

Sin embargo, nadie conoce ese algoritmo excepto el personal del productor.

Es posible que el algoritmo de activación esté configurado para activar el jackpot durante el día; nadie puede excluir esta posibilidad.

Incluso para los progresivos que deben golpear antes de un monto específico, donde se supone que el algoritmo permite que el RNG elija solo sobre una distribución de los valores del contador, no podemos saber con certeza si este es el único factor. Por lo tanto, jugar de noche no vale la pena el esfuerzo de intentar ganar el jackpot, especialmente en esos sistemas donde se requiere alcanzar el jackpot regular para ser elegible para el jackpot.

La probabilidad de este último evento es lo suficientemente baja y la misma tanto de día como de noche.

Mito 4: Si una máquina acaba de pagar, es poco probable que pague en los próximos giros. Si una máquina no ha pagado durante mucho tiempo, es probable que pague pronto

Hecho: Ninguna de estas afirmaciones es verdadera, cualquiera que sea el RTP y la volatilidad de una máquina.

La probabilidad, el RTP, la varianza, son todos promedios estadísticos teóricos que solo se materializan a largo plazo. Es físicamente posible que una máquina no pague en ningún número de giros.

Además, los giros son independientes entre sí y el RNG elige miles de números por segundo, de los cuales solo uno determina el resultado. Cada fracción de segundo que demoras en presionar el botón de giro resulta en un resultado diferente del giro.

Por lo tanto, no hay razón racional para que un jugador se enoje cuando alguien gana un jackpot u otro tipo de premio en una máquina que acababa de jugar, ni para elegir una máquina solo porque no ha pagado nada o ha pagado muy poco durante un largo período de tiempo.

Mito 5: Cualquier máquina tragamonedas eventualmente te devolverá el porcentaje indicado por su RTP si no obtienes premios.

Hecho: El RTP, como promedio estadístico, no se aplica a tu propio juego, sino a la actividad de todos los jugadores en esa máquina, a lo largo del tiempo. El reembolso de una máquina tragamonedas no se distribuye por ninguna regla sobre la sesión de juego de uno y no se distribuye uniformemente a lo largo del tiempo sobre todos los giros, al igual que los resultados ganadores tampoco lo son.

The payback of a slot machine is not distributed by any rule over one’s session of play and is not uniformly distributed over the long run over all spins, just like the winning outcomes are not. 

Mito 6: Actuar sobre la palanca o el botón de giro de cierta manera o en un cierto momento te da cierto control sobre los resultados.

Hecho: Esta ilusión de control no tiene nada que ver con cómo funciona una máquina tragamonedas, ya sea que hablemos de tragamonedas mecánicas, electromecánicas o de carretes virtuales.

Para las tragamonedas mecánicas, las características de su mecanismo aseguran la aleatoriedad de los resultados.

Para las tragamonedas con RNG, es el RNG el que determina el resultado incluso antes del momento en que el botón de giro activa el giro mecánico o virtual.

Conclusión

Las tragamonedas son un juego de casino especial en cuanto a transparencia.

La configuración paramétrica del juego se mantiene en secreto por los productores de juegos y solo puede ser recuperada a través de un esfuerzo de seguimiento estadístico o por intervención legal. El diseño interno del juego de las tragamonedas tiene parámetros que pueden ser manipulados en el momento de la concepción para producir casi-aciertos artificiales.

Los indicadores estadísticos de un juego – probabilidades de ganar, RTP, ventaja de la casa, volatilidad – no pueden ser estimados con precisión en ausencia de los datos sobre la configuración paramétrica de un juego. Los únicos indicadores que suelen exponerse son el RTP y el índice de volatilidad.

Estos indicadores pueden servir como criterios para elegir un juego u otro, pero no tienen ningún papel estratégico, excepto en el caso de los progresivos que deben golpear antes de un monto específico, donde jugar después del punto de equilibrio es una estrategia basada en expectativas donde el RTP está involucrado junto con el valor máximo del jackpot.

Las probabilidades de ganar el jackpot regular y otros premios principales son diminutas y la probabilidad de alcanzar el jackpot progresivo es aún menor, en el orden de 1 en millones a 1 en decenas de millones o más.

Perseguir un jackpot progresivo es una elección arriesgada, cualquiera sea la estrategia y el saldo utilizado.

Las tragamonedas son reconocidas por los expertos en problemas de juego como el juego de casino con mayor potencial de volverse adictivo.

Por esta razón, un primer requisito para un juego responsable en las tragamonedas es informarse sobre cómo funcionan realmente las tragamonedas y cómo están diseñadas matemáticamente, para resistir todo tipo de ilusiones y conceptos erróneos específicos sobre el juego.

Referencias

• Bărboianu, C. (2013). The mathematics of slots: Configurations, combinations, probabilities. Craiova: Infarom.
• Bărboianu, C. (2019). The epistemology of the near miss and its potential contribution in the prevention and treatment of problem-gambling. Journal of Gambling Studies, Vol. 35, 1063-1078.
• Bărboianu, C. (2022). Understanding your game: A mathematician’s advice to rational and safe gambling. PhilScience Press.
• Beresford, K., & Blaszczynski, A. (2020). Return-to-player percentage in gaming machines: Impact of informative materials on player understanding. Journal of Gambling Studies, 36(1), 51-67.
• Harrigan, K. A. (2007). Slot machine structural characteristics: Distorted player views of payback percentages. Journal of Gambling Issues, Vol. 20, 215-234.
• Harrigan, K. A. (2008). Slot Machine Structural Characteristics: Creating Near Misses Using High Award Symbol Ratios. International Journal of Mental Health and Addiction, Vol. 6, 353-368.
• Harrigan, K. A., & Dixon, M. (2009). PAR Sheets, probabilities, and slot machine play: Implications for problem and non-problem gambling. Journal of Gambling Issues, Vol. 23, 81-110.
• Kilby, J., Fox, J. & Lucas, A. F. (2005).  Casino Operations Management. Wiley.
• Turner, N. E., & Horbay, R. (2004). How do slot machines and other electronic gambling machines really work? Journal of Gambling Issues, Vol. 11. 
• Turner, N. E. (2011). Volatility, house edge and prize structure of gambling games. Journal of Gambling Studies, 27(4), 607-623.