Las probabilidades de bacará desmitificadas: Entendiendo las matemáticas detrás de la ventaja de la casa

Domina las probabilidades y la ventaja de la casa en el bacará (o baccarat) utilizando las ideas expertas del Dr. Catalin Barbioanu. En esta guía, él desmitifica las complejidades de las matemáticas detrás del bacará.

Aquí te mostramos cómo este artículo te ayudará a optimizar tu juego y aumentar tu potencial de ganar:

• Qué es el baccarat
• Apuestas de bacará y sus probabilidades de pago
• Probabilidades básicas y ventaja de la casa en el bacará
• Probabilidades y ventaja de la casa para las apuestas secundarias
• Mejorando las probabilidades de ganar en bacará
• Cómo cambia la ventaja de la casa con diferentes variantes de bacará
• Las probabilidades de rachas en el bacará

Profundizando en las matemáticas detrás de este popular juego de casino, el Dr. Barbioanu desglosa con maestría las probabilidades de cada resultado, ya sea jugador, Banca o empate.

Con una explicación clara de la ventaja de la casa para cada apuesta y cómo afecta tus posibilidades de ganar, este artículo sirve como un recurso valioso tanto para los entusiastas del bacará como para los principiantes.

Sigue leyendo para aprender más.

¿Qué es el baccarat?

El juego de bacará se parece en muchos aspectos al blackjack, pero solo en lo que respecta al movimiento de las cartas y al objetivo de alcanzar un valor total más alto que el del otro lado.

El bacará se juega generalmente con uno, seis u ocho mazos de cartas repartidos desde una caja, usualmente con ocho mazos.

La gran diferencia es que en el bacará no apuestas a tu mano, sino a la mano de un banco imaginario o a la mano del jugador, que en realidad juega el crupier.

Por lo tanto, el juego de bacará es una apuesta secundaria en sí misma y, por lo tanto, más simple que el blackjack.

Esta característica hace que cualquier juego estratégico en el bacará sea menos complejo que en el blackjack. Por otro lado, a diferencia del blackjack, donde superar los 21 puntos te saca del juego, en el bacará no existe la posibilidad de bust debido a la regla de eliminar el primer dígito de un total mayor que 10.

Esta regla hace que, en ciertos aspectos, las matemáticas del bacará sean más complejas que las del blackjack en lo que respecta a los cálculos de probabilidades.

Exploremos las probabilidades, las ventajas de la casa y los márgenes de ganancia asociados con el juego del baccarat y sus versiones.

Apuestas de bacará y sus probabilidades de pago

Hay tres tipos de apuestas disponibles en el bacará: en el banco, en el jugador o en un empate.

• La apuesta al jugador paga de manera uniforme (1 a 1).
• La apuesta al banco paga de manera uniforme, pero la casa retiene una comisión habitual del 5% para esta apuesta, por lo que las probabilidades reales de pago son 19 a 20.
• La apuesta al empate generalmente paga 8 a 1 (o 9 a 1 en algunos casinos)

Para la apuesta al banco, las probabilidades de pago se muestran en la tabla a continuación como 1:1; debes tener en cuenta que son menores debido a la comisión retenida.

Algunos casinos también tienen una apuesta de par en el programa del juego base (otros la tienen como una apuesta secundaria), que gana si el jugador o el banco (según lo nomine el apostador) tienen un par de cartas del mismo valor (generalmente paga 5 a 1).

Apuesta	Probabilidades de pago
Jugador	1 a 1
Banco	19 a 20
Empate	8 a 1 (9 a 1)

Estas probabilidades de pago aproximan las probabilidades de que ocurran los eventos respectivos, como “probabilidades reales” o probabilidades: las probabilidades de que el banco gane son ligeramente mayores que las del jugador, mientras que las probabilidades de un empate son las más bajas.

La razón es que el banco se beneficia de una ventaja posicional, con más información disponible para decidir si toma una tercera carta. La diferencia entre las probabilidades de pago y las probabilidades reales le da a la casa una ventaja o margen de ganancia.

Algunos jugadores pueden considerar el baccarat un juego aburrido debido a su simplicidad y al número muy limitado de apuestas básicas (tres).

Es por eso que los casinos han mejorado el juego con las llamadas apuestas secundarias, es decir, apuestas realizadas sobre la configuración y características del resultado final del juego, además de quién gana o el empate.

Como en muchos otros juegos de azar, en el bacará los jugadores tienen la oportunidad de realizar apuestas secundarias, que son opcionales y varían de un casino a otro, y también varían según la versión del juego.

Estas apuestas secundarias incluyen:

• Bono Dragón: Comúnmente ofrecido en Mini bacará. Apostar a que cualquier mano logre un máximo de 9 puntos. Paga 30 a 1;
• Panda 8: Comúnmente ofrecido en EZ bacará. Apostar a que la mano de el banco logre 8 puntos con tres cartas. Paga 25 a 1;
• Dragón 7: Comúnmente ofrecido en EZ bacará. Apostar a que la mano de el banco logre 7 puntos con tres cartas. Paga 40 a 1;
• Par: Apostar a que las dos cartas repartidas al jugador o el banco (según lo nomine el apostador) formen un par. Paga 5 a 1;
• Pares: Apostar a que las dos cartas repartidas al jugador y a el banco formen un par. Paga 11 a 1 (o 10 a 1);
• Par Perfecto: Ofrecido en el bacará en línea ofrecido por Playtech. Apostar a que la mano inicial del jugador o de el banco forme un par, con diferentes probabilidades de pago para par con o sin palo. Algunas plataformas requieren que este par sea del mismo palo, con probabilidades de pago únicas. Tiene diferentes pagos: 5 a 1, si el par no es del mismo palo, 25 a 1, si el par es del mismo palo, y 12 a 1 probabilidades de pago únicas si el par es del mismo palo)
• Todo Rojo/Todo Negro: Apostar a que la mano del jugador consista únicamente en cartas rojas (diamantes y corazones) o negras (espadas y tréboles). Paga 22 a 1 (todo rojo), 24 a 1 (todo negro).
• Egalité: Apostar al valor exacto del resultado del empate. Los pagos son diferentes: 80 a 1 (valor empatado 9 o 8), 45 a 1 (valor empatado 7 o 6), 110 a 1 (valor empatado 5), 120 a 1 (valor empatado 4), 200 a 1 (valor empatado 3), 225 a 1 (valor empatado 2), 215 a 1 (valor empatado 1), 150 a 1 (valor empatado 0).
• Natural 8: Apostar a que el banco o el jugador tengan un total natural de 8. Paga 9 a 1 (o 8 a 1).
• Natural 9: Apostar a que el banco o el jugador tengan un total natural de 9. Paga 9 a 1 (o 8 a 1).
• Natural 8 o 9: Apostar a ambos números. Paga 4 a 1.

Existen algunas otras apuestas secundarias, pero no son tan populares. Las apuestas mencionadas anteriormente son las más comunes que encontrarás.

Probabilidades básicas y ventaja de la casa en baccarat

Las probabilidades de los diversos eventos en el bacará son probabilidades combinatorias y se calculan mediante fórmulas compactas, métodos recursivos o simulaciones por computadora, dependiendo de la complejidad del evento.

La probabilidad de un evento en el bacará es la relación entre el número de combinaciones de cartas para las manos de el banco y del jugador (la configuración de cartas de la mesa cuando el juego ha terminado) que son favorables para que ocurra ese evento y el número total de combinaciones de cartas posibles para ambas manos.

La ventaja de la casa en una apuesta de bacará es lo contrario (como signo +/–) de su valor esperado en relación con la apuesta inicial.

Refleja la proporción de las apuestas que va a la casa como ganancia de tus apuestas a lo largo del tiempo. En las ecuaciones del valor esperado y la ventaja de la casa se emplean las probabilidades de ganar y perder la apuesta y las probabilidades de pago de la apuesta.

Las probabilidades de ganar (para las apuestas básicas y secundarias) varían con el número de mazos utilizados. En las tablas a continuación se muestran las probabilidades de las apuestas básicas junto con su ventaja de la casa para ocho, seis y un mazo, para una comisión estándar del 5% en la apuesta de el banco.

Apuesta al banco — 8 Mazos

Apuesta al jugador — 8 Mazos

Apuesta al empate — 8 Mazos

Apuesta al banco — 6 Mazos

Apuesta al jugador — 6 Mazos

Apuesta al empate — 6 Mazos

Apuesta al banco — 1 Mazo

Apuesta al jugador — 1 Mazo

Apuesta al empate — 1 Mazo

Como se puede ver, existen ligeras diferencias en la probabilidad del mismo evento para los tres casos, y también en lo que respecta a la ventaja de la casa.

Entre las tres apuestas básicas, la apuesta a el banco ofrece el mayor rendimiento y, en consecuencia, la menor ventaja de la casa, mientras que la apuesta al empate (la más arriesgada) tiene la mayor ventaja de la casa, entre 14.35% y 15.76%.

También podemos estimar una ventaja de la casa global al hacer el promedio estadístico de las ventajas de la casa de cada apuesta.

Tal indicador solo es relevante bajo el supuesto de que los tipos de apuestas se distribuyen uniformemente a lo largo del tiempo (lo que, por supuesto, no sucede en la práctica, ya que la apuesta a el banco es la más frecuente). Por ejemplo, en el caso de un juego de 8 mazos, la ventaja de la casa general es del 2.40%.

Con solo un 1.06% de ventaja de la casa para la apuesta a el banco, el bacará es uno de los juegos de casino que ofrece el mayor rendimiento, siendo superado solo por el blackjack jugado con estrategia, con una ventaja de la casa inferior al 1%.

El consejo estratégico más popular en el bacará es apostar solo a el banco debido a esa ligera diferencia en la probabilidad de ganar en comparación con la apuesta al jugador.

Este consejo puede ampliarse con la recomendación de realizar la apuesta a el banco en un juego de 1 mazo debido a otro ligero aumento en la probabilidad a favor de este último juego. Sin embargo, los efectos de tales elecciones pueden ser visibles solo en un período muy largo de juego, o en absoluto.

Probabilidades y ventaja de la casa en apuestas secundarias

Las apuestas secundarias en baccarat tienen sus propias probabilidades y ventaja de la casa, que dependen del número de barajas utilizadas (como en el caso de las apuestas base). El número de posibles apuestas secundarias es grande y muchas de ellas están asociadas con una cierta versión de bacará.

En esta sección, solo proporcionamos las cifras asociadas con la apuesta de Pareja, la apuesta Panda 8, la apuesta Egalité, la apuesta Natural 8, la apuesta Natural 9 y la apuesta Natural 8 o 9.

Probabilidades de apuesta de pareja — 8 Mazos

Probabilidades de apuesta de pareja — 6 Mazos

Probabilidades de Apuesta de Pareja — 1 Mazo

El Panda 8 es una apuesta secundaria en EZ bacará (donde no hay comisión en las apuestas ganadoras de  banco y una apuesta ganadora en  banco con un siete de 3 cartas será un empate; el EZ baccarat se juega con 6 u 8 barajas, usualmente 8). La apuesta Panda 8 paga 25 a 1 para un total ganador de 8 en 3 cartas para el jugador.

Probabilidades de Panda 8 (8 Mazos)

Probabilidades de Egalité (8 Mazos)

Natural 8 — Pago de 9 a 1 (8 Mazos)

Natural 8 — Pago de 8 a 1 (8 Mazos)

Natural 9 — Pago de 9 a 1 (8 Mazos)

Natural 9 — Pago de 8 a 1 (8 Mazos)

Natural 8 o 9

A diferencia de las apuestas base, en las apuestas secundarias generalmente existen grandes diferencias en la ventaja de la casa entre las versiones del juego jugadas con 8, 6 o 1 baraja.

Podemos ver que en la apuesta de Pareja, la ventaja de la casa aumenta del 10.36% para 8 barajas al 29.41% para 1 baraja. Sin embargo, la probabilidad de ganar no sigue el mismo ritmo de aumento: de 7.46% a 5.88% respectivamente.

Regla de la tercera carta explicada – Cómo y por qué

El bacará es conocido como uno de los juegos de casino más simples en cuanto a jugar y apostar.

Sin embargo, lo único que a veces lo hace parecer complicado es la llamada regla de la tercera carta, que se utiliza para determinar si la mano del jugador o del banco termina la ronda con dos o tres cartas.

La regla es bastante sencilla cuando se trata de la mano del jugador, que consiste en las dos primeras cartas reveladas en la mesa en cada ronda. Sin embargo, que el banco reciba una tercera carta depende de todas las cartas reveladas actualmente en la mesa.

El jugador recibe una tercera carta solo dependiendo del total de las dos primeras cartas del jugador:

 

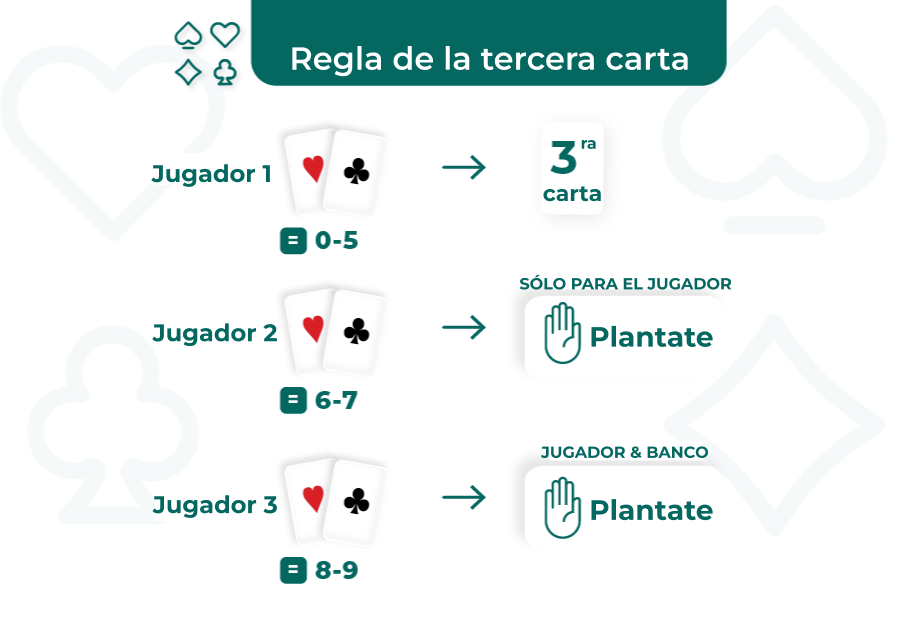
• (p1) Si las dos primeras cartas del jugador suman un total de 0-5, al jugador se le reparte una tercera carta.
• (p2) Si las dos primeras cartas del jugador suman 6 o 7, el jugador se planta y no se reparte una tercera carta.
• (p3) Si las dos primeras cartas del jugador suman 8 o 9, tanto el jugador como el banco se plantan con dos cartas.
• (b0) Si el jugador se planta con solo dos cartas, las mismas reglas de la tercera carta se aplican al lado del banco. (El banco saca una tercera carta si el total de las dos primeras cartas es 0-5).

 

Si el jugador tiene tres cartas en la mesa, las cosas se complican un poco con un nuevo conjunto de reglas:

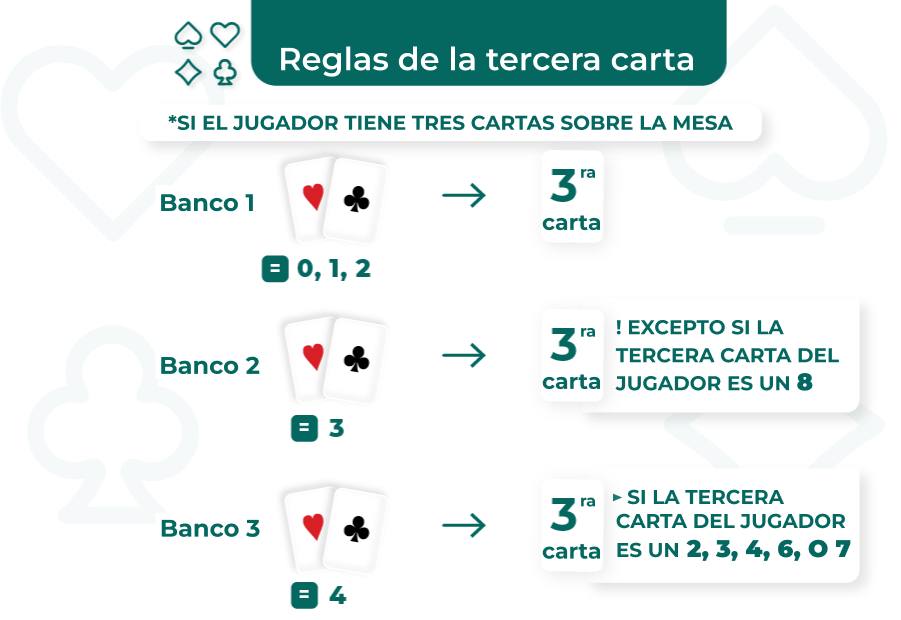
• (b1) Si las dos primeras cartas del banco suman 0, 1 o 2, el banco siempre saca una tercera carta.
• (b2) Si las dos primeras cartas del banco suman 3, se saca una tercera carta en todos los casos, excepto si la tercera carta del jugador es un 8.
• (b3) Si las dos primeras cartas del banco suman 4, se saca una tercera carta si la tercera carta del jugador es 2, 3, 4, 5, 6 o 7.
• (b4) Si las dos primeras cartas del banco suman 5, se saca una tercera carta si la tercera carta del jugador es 4, 5, 6 o 7.
• (b5) Si el total del banco es 6, se saca una tercera carta si la tercera carta del jugador es 6 o 7.
• (b6) Si el banco tiene un total de 7, 8 o 9 con las dos primeras cartas, no se reparte una tercera carta.

Este conjunto de reglas de la tercera carta para el banco en la situación donde el jugador tiene una mano de tres cartas generalmente se resume en una tabla que verás en casi cualquier guía de bacará.

Pero, ¿cuál es la razón detrás de esta "compleja" regla de la tercera carta?

Primero, recuerda que el enfrentamiento banco-jugador es solo ilusorio; en realidad, el crupier está jugando ambos roles y las dos manos que el banco y el jugador terminan el juego son, de hecho, partes de un solo resultado del juego (una combinación de cuatro, cinco o seis cartas).

Sin embargo, dado que el crupier actúa como dos "jugadores", sería injusto favorecer significativamente a un lado u otro y esto también sería contraproducente para el juego, ya que el apostador apostaría constantemente en el lado que tenga mayores posibilidades de ganar; la ventaja de la casa se volvería negativa y el juego dejaría de ser rentable.

Al mantener esa diferencia baja, se anima a los apostadores a apostar de manera uniforme.

Además, el jugador, como un jugador real, tendría la opción de elegir si plantarse o pedir otra carta; dado que este no es el caso, la regla de la tercera carta elimina esta opción.

Al igual que en el blackjack, donde los jugadores no están obligados por ninguna regla a plantarse en un total determinado, en bacará solo se les permite tomar una carta adicional según las reglas de la tercera carta.

Como vimos en las secciones anteriores, la diferencia en la probabilidad de ganar (estimada antes de que se reparta cualquier carta) no es grande entre el banco y el jugador y esta es una característica específica del juego de bacará.

Desde el punto de vista del jugador y dado que al jugador se le reparte antes que al banco, según la regla de la tercera carta, el jugador tiene la oportunidad de mejorar su total, ya que no "sabe" cuál será la mano del banco.

En la siguiente tabla se indican las probabilidades de ganar para ambos lados en función de las dos primeras cartas repartidas al jugador.

Probabilidades de ganar después de repartir dos cartas al jugador (8 barajas)

Observa que para un total de 0 a 5, la probabilidad de que el jugador gane es mucho menor que la probabilidad de que gane el banco, sin mencionar las probabilidades de empate, que juegan en contra del apostador que apuesta al jugador.

Esto explica la regla de que al jugador se le reparta una tercera carta en esta situación (p1). Con un total de 6, las probabilidades se vuelven casi iguales, sin contar el empate, mientras que para un total de 7, se invierten significativamente. Esto explica por qué el jugador está obligado a plantarse con un total igual o superior a 6 (reglas p2 y p3).

Además, 0 es el valor más probable que proviene de una sola carta. Eso se debe a que los 10, Jotas, Reinas y Reyes cuentan como 0, por lo que es cuatro veces más probable que cualquier otro valor. En otras palabras, el jugador probablemente terminará en el mismo lugar donde comenzó después de sacar la tercera carta.

Incluso si el jugador solo saca la tercera carta con manos débiles, es probable que la mano sea más débil después de sacar que antes.

Por ejemplo, si una mano tiene un total de 5, las únicas cartas que realmente harán que esa mano sea más fuerte son 1, 2, 3 y 4. Todo lo demás reduce el valor de la mano o lo mantiene igual.

Ahora pasemos al banco. La lógica detrás de la regla de la tercera carta en relación con el banco sigue el principio de que el banco solo saca la tercera carta cuando le conviene. Si fuera un jugador real, esta sería la acción natural.

Otro principio es que la pequeña ventaja del banco sobre el jugador, reflejada en las probabilidades y la ventaja de la casa de una apuesta en banco, debe mantenerse. Según este principio, el banco solo saca la tercera carta si tiene una mano desfavorable en comparación con el jugador, es decir, solo si no está a punto de ganar la mano actual.

Probabilidad de que el jugador gane después de repartir cuatro cartas (dos para el jugador y dos para el banco) (8 barajas)

Si el jugador tiene un total de 6 o 7 y el banco tiene entre 0 y 5, obviamente una tercera carta favorece al banco, aunque la probabilidad de que el jugador gane sea alta (destacada en la tabla anterior con rojo oscuro). Observe en la tabla que, para un total de 0 a 5 tanto para el banco como para el jugador, la probabilidad de que el jugador gane si el banco saca una tercera carta es superior al 50% en solo nueve de los casos (destacados en azul en la tabla).

En el resto de los casos, es más probable que gane el banco o que haya un empate. Esto expresa la ventaja general del banco si saca una tercera carta y, como tal, justifica la regla b0. A pesar de las excepciones señaladas, la regla hace justicia para ambos lados en lo que respecta a la regla básica de sacar una tercera carta con un total de 0 a 5.

Probabilidad de que el jugador gane después de repartir cinco cartas (tres para el jugador y dos para el banco) (8 barajas)

Si el banco tiene un total de 0 a 2 y el jugador tiene un total de 4 a 9, sacar una tercera carta favorece al banco, aunque el jugador tenga una alta probabilidad de ganar la mano.

Si el total del jugador es de 0 a 4, la probabilidad general de que el banco o un empate ganen si el banco saca una tercera carta es mayor que la probabilidad de que gane el jugador.

Esto justifica la regla b1.

Mirando toda la tabla, podemos ver que es favorable para el banco sacar una tercera carta en casi todas las situaciones, excepto cuando el banco tiene un total superior a 6, menor que el total del jugador, lo que le impide sacar una carta según las reglas b5 y b6. Sin embargo, las situaciones en las que la probabilidad de que el jugador gane si el banco saca la tercera carta es superior al 50% son casi la mitad del total de las situaciones.

Esto significa que, aunque el banco tiene la ventaja de tener la oportunidad de sacar la tercera carta, esa ventaja no es estadística (podría materializarse solo en aproximadamente la mitad de las situaciones).

Las reglas b3 a b5 contribuyen a mantener la ventaja del banco en términos estadísticos. Cuando el total del banco está entre 3 y 6, sacar una tercera carta probablemente lo degradará.

Restringir la extracción por la tercera carta del jugador equilibra nuevamente la ventaja general del banco.

Las condiciones en las reglas b3 a b5 son en realidad arbitrarias, ya que no es una carta específica la que cuenta hacia la probabilidad de ganar, sino todas las cartas en la mano del jugador.

Sin embargo, en su conjunto, están elegidas tomando en cuenta probabilidades específicas asociadas con toda la mano, que son muy difíciles de calcular manualmente.

La regla b6 nuevamente consolida la ventaja del banco, ya que un total de 7, 8 o 9 le da las mayores probabilidades de ganar.

Todo el conjunto de reglas para la tercera carta está diseñado para mantener la ventaja del banco sobre el jugador, pero las reglas están elegidas de manera que esta ventaja sea mínima, como se refleja en el balance de probabilidades 45.86% (para el banco) – 9.51% (para un empate) – 44.62% (para el jugador), para un juego de bacará con 8 barajas, y la ventaja de la casa del 1.05% para una apuesta en el banco.

Mejorando las probabilidades de ganar en bacará

La similitud entre el blackjack y el bacará también se refleja en la respuesta a la pregunta de si las probabilidades de ganar en baccarat se pueden mejorar.

Teóricamente, estas probabilidades pueden mejorarse, pero solo en ciertas condiciones y mediante una estrategia de conteo de cartas, como en el blackjack.

La única información posible está disponible cuando se juegan múltiples manos antes de que se mezcle la baraja. Con cada carta repartida, cambian las probabilidades de que gane un lado u otro (o que haya un empate).

Esto significa que al observar las cartas repartidas y usar un algoritmo de conteo, puedes encontrar cuándo las probabilidades favorecen a un lado u otro.

El conteo de cartas en blackjack es conocido por ser efectivo (aunque difícil de poner en práctica) al reducir la ventaja de la casa y proporcionar una expectativa positiva en ciertas situaciones.

La pregunta es hasta qué punto es efectiva una estrategia de conteo de cartas en bacará. Primero, veamos cuál es el efecto de eliminar una carta de la baraja sobre las probabilidades. 

Probabilidad después de eliminar una carta (8 barajas)

Podemos ver que las probabilidades iniciales no cambiaron mucho con una carta eliminada.

Ventaja de la casa después de eliminar una carta (8 barajas)

Podemos ver que la ventaja de la casa tampoco cambió mucho con una carta eliminada, pero hay situaciones en las que aumentó y otras en las que disminuyó. El efecto de la eliminación de cartas sobre la ventaja de la casa se muestra en la siguiente tabla, donde un signo negativo indica una disminución y un signo positivo un aumento:

Efecto de la eliminación de cartas en la ventaja de la casa (8 barajas)

Las situaciones con disminución (negativo) indican una ventaja para la apuesta al jugador, mientras que aquellas con aumento (positivo) indican una ventaja para la apuesta al banco. Cualquier nueva carta repartida puede aumentar o disminuir esta ventaja.

Como en el blackjack, una medida objetiva para esta ventaja se obtiene mediante el conteo de cartas, que es un algoritmo que opera con valores asociados a cada carta para proporcionar un valor general final (el conteo en curso).

Luego, el conteo en curso se divide por el número de cartas restantes en la baraja para obtener la medida final que indicará qué apuesta es ventajosa (el conteo real).

Existen varios sistemas de conteo de cartas para bacará (como los hay para blackjack), sobre los cuales puedes leer en la mayoría de las guías de estrategia de bacará.

También existen varias estrategias para utilizar el conteo en curso o real. Para ciertos valores del conteo en curso y estrategias, la ventaja de la casa en tu apuesta en bacará puede reducirse en relación con su valor estándar (asociado al juego no estratégico).

La tabla anterior muestra el efecto en la ventaja de la casa de solo una carta eliminada, pero el efecto acumulado aumenta con cada carta repartida. Una estrategia óptima es aquella en la que explotas las situaciones asociadas con los valores favorables de la ventaja de la casa, es decir, apuestas en el banco, el jugador o empate, o retienes tu apuesta y esperas el próximo valor favorable.

El conteo real puede indicar situaciones en las que la ventaja de la casa supera el punto cero, es decir, la expectativa de esa apuesta es positiva.

Esto no significa que ciertamente ganarás esa apuesta en esa instancia particular, sino que puedes esperar un beneficio positivo a largo plazo si juegas de esa manera cada vez que ocurre esa situación.

La siguiente tabla muestra la proporción de manos jugadas, basada en una simulación de 100 millones, en las que el conteo real supera el punto cero de la ventaja de la casa. La columna de la izquierda indica la proporción de cartas repartidas antes de que se barajen las cartas.

Expectativa positiva

Si hablamos en términos de ganancias, los valores de la tabla anterior aplicados a 100 apuestas y una inversión de $1,000 cada vez que ocurra un valor esperado positivo dan la siguiente tabla:

Ganancia esperada para el juego óptimo basado en expectativa positiva

Sin necesidad de más cálculos, se puede ver cuán baja es la tasa de ganancias en este juego estratégico.

Sin embargo, el juego estratégico basado en el conteo de cartas reduce la ventaja de la casa, pero no tanto.

Por ejemplo, con una estrategia básica, la ventaja de la casa en la apuesta al banco se reduce a 0.99% en comparación con la ventaja de la casa del 1.06% para esa apuesta cuando no se cuentan cartas.

La recomendación estratégica general y simplista de siempre apostar al banco se mantiene mientras no se emplee el conteo de cartas; sin embargo, incluso una simple observación de que se han repartido muchas cartas altas (de modo que el mazo sigue siendo rico en cartas bajas) indica que el jugador tiene ventaja y la recomendación cambia.

Ahora, dejando de lado las cifras, recuerda que un juego óptimo estratégico asume que el jugador es capaz de mantener un conteo perfecto y aplicarlo, y que tanto el jugador como el casino no se van a molestar si el jugador sólo hace una apuesta una vez cada decenas o cientos de manos.

Por ejemplo, si se sigue la estrategia de solo expectativa positiva, se debería realizar una apuesta en 475 manos o menos.

Sumando a esto la baja tasa de ganancias, queda claro que el juego de conteo de cartas, aunque matemáticamente óptimo, no es efectivo en la práctica, ya que es inconveniente, en el sentido de que los resultados acumulados no valen el esfuerzo para lograrlos; además, simplemente cancelaría la diversión de jugar el juego.

La efectividad del conteo de cartas es diferente en el blackjack, donde los valores de las expectativas positivas (cuando ocurren) son mucho más altos, y la reducción general de la ventaja de la casa es mayor que en el bacará.

Cómo cambia la ventaja de la casa con diferentes variantes de bacará

Como en cualquier juego de azar, cualquier modificación en las reglas o en la tabla de pagos del juego afecta ya sea las probabilidades de los eventos ganadores o los indicadores estadísticos del juego, como la expectativa y la ventaja de la casa (o ambos).

Existen varias versiones de baccarat con respecto al juego básico (sin tener en cuenta las apuestas secundarias). Una categoría de versiones se da por la comisión en la apuesta al banco, que puede variar con valores inferiores al 5%.

La siguiente tabla muestra la ventaja de la casa en la apuesta al banco dependiendo de la comisión y el número de mazos utilizados.

Ventaja de la casa en la apuesta al banco

Algunos casinos (principalmente en el Reino Unido) tienen una regla de Red 8, donde las apuestas ganadoras al banco no pagan comisión en ciertas victorias. Algunos tienen una regla de Red 8 donde las apuestas al banco pagan 1 a 1 si:

El banco tiene un total de tres puntos con dos cartas.

El jugador tiene un total de cinco puntos o menos con dos cartas.

La tercera carta del jugador es un 8.

Suponiendo ocho mazos, esta regla reduce la ventaja de la casa en la apuesta al banco del 1.06% al 0.81%.

Probabilidades y ventaja de la casa para la apuesta al banco bajo la regla de Red 8 (8 mazos)

Existen varias versiones de bacará sin comisión. La versión más popular es el EZ bacará. Sus reglas siguen el bacará estándar excepto en la apuesta al banco:

1. todas las victorias pagan dinero parejo,
2. si el banco gana con un total de tres cartas de 7, entonces la apuesta al banco será un empate.

La siguiente tabla muestra la ventaja de la casa en las apuestas al banco en EZ bacará. La ventaja general de la casa es 1.02%.

Probabilidades y ventaja de la casa para la apuesta al banco en EZ bacará (8 mazos)

Otra versión de bacará sin comisión es el Monkey bacará. Como en EZ bacará, la apuesta al banco paga 1 a 1, excepto en una victoria con un total de tres cartas de 7, cuando la apuesta al banco es un empate.

La siguiente tabla muestra las probabilidades y la ventaja de la casa para la apuesta al banco en Monkey bacará. La ventaja general de la casa en esta apuesta es 1.02%.

Probabilidades y ventaja de la casa para la apuesta al banco en Monkey bacará (8 mazos)

Otra versión de bacará sin comisión es el Nepal Baccarat. Esta variante de bacará sigue las reglas convencionales, con la siguiente excepción: una apuesta ganadora al banco paga dinero parejo, excepto con un total ganador de seis, cuando pagan 1 a 2. La ventaja de la casa en las apuestas al jugador y al empate es la misma que en el bacará convencional. La ventaja de la casa en la apuesta al banco es 1.46%.

La siguiente tabla muestra las probabilidades y la ventaja de la casa para la apuesta al banco en Nepal Baccarat.

Probabilidades y ventaja de la casa para la apuesta al banco en Nepal Baccarat (8 mazos)

Cambiar las probabilidades de pago para la apuesta al empate da una nueva versión de bacará. El empate paga 9 a 1 en algunos casinos. La ventaja de la casa de la apuesta al empate que paga 9 a 1 es:

• Para 8 mazos: 4.844%
• Para 6 mazos: 4.931%
• Para 1 mazo: 6.385%

Las probabilidades de rachas en bacará

Con solo tres apuestas básicas para elegir, un apostador regular o simplemente un observador del juego verá, por supuesto, a veces la misma apuesta ganar varias veces seguidas (evento llamado racha en la jerga de los juegos de azar).

Cuando esto sucede, uno puede preguntarse, por supuesto, cuáles son las probabilidades de que eso ocurra. Por ejemplo, ¿cuáles son las probabilidades de que el banco gane cuatro veces seguidas?

Esa información no tiene relevancia matemática ni estratégica, ya que los juegos son independientes entre sí.

Además, para aquellos que juegan sistemas progresivos como el martingala, conocer estas probabilidades podría alimentar la distorsión cognitiva conocida como la falacia del jugador.

Sin embargo, por el bien de la información, presento las probabilidades de las rachas en bacará en la siguiente tabla.

Probabilidad de rachas en bacará (6 mazos)

Las cifras se aplican a cualquier punto de partida para la racha (no importa si es en el primer, segundo, tercer juego, etc.). El empate no fue incluido.

El bacará es un juego similar en muchos aspectos al blackjack, pero también muy diferente.

El bacará está junto al blackjack en la categoría de juegos de azar con la menor ventaja de la casa. En cuanto a las apuestas, el bacará es un juego muy sencillo, ofreciendo tres apuestas básicas, cuyas probabilidades y ventajas de la casa pueden memorizarse fácilmente.

Sin embargo, estos parámetros cambian con la variante del juego, incluyendo los diversos números de mazos de cartas utilizados. Esta simplicidad se ve contrarrestada por las apuestas secundarias que muchas variantes ofrecen.

Las probabilidades del bacará asociadas con las apuestas secundarias son muy diferentes de las de las apuestas básicas (las probabilidades de ganar son mucho menores y las probabilidades de pago son mucho mayores en consecuencia).

Lo único complicado del bacará es la regla de la tercera carta, que se justifica por cálculos precisos de probabilidad y cuyo propósito es mantener la ventaja del banco sobre el jugador con una ventaja mínima.

El juego estratégico es posible en el bacará y se basa en el conteo de cartas, como en el blackjack, sin embargo, es mucho menos efectivo que en el blackjack, dado las tasas de ganancias muy bajas y las largas sesiones de espera para realizar las apuestas.

Aunque la información matemática expresada en probabilidades y ventaja de la casa no ofrece ayuda estratégica práctica en bacará, informarse sobre estas cifras es importante para aquellos que juegan regularmente con el fin de obtener ganancias más que por diversión.

Para estos jugadores habituales, estos indicadores matemáticos son criterios objetivos para elegir un juego u otro o para elegir entre varias variantes del mismo juego.