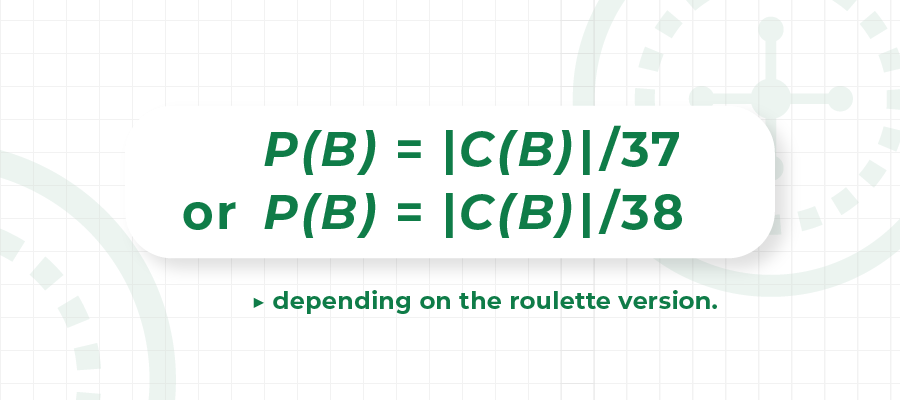Roulette is one of the oldest casino games and the simplest to understand and play. You don’t need advanced math knowledge to grasp roulette probabilities and other mathematical notions applied in this game and its strategies.
Invented by mathematician Blaise Pascal (the early father of probability theory) in the 18th century, it is also the most straightforward casino game with respect to roulette odds computations.
Played in its contemporary form for over 220 years, we can grant roulette another superlative besides simplicity, namely transparency.
In this game, the possible outcomes are visible and countable on the roulette wheel. It is possible to calculate the odds of winning any particular bet (contrary to other games of chance, such as slots).
Be aware
Despite such virtues, roulette is yet a game in which many players fall into the trap of false or irrational beliefs, fallacies, and misconceptions.
Such situations can be avoided when players know the mathematical facts behind roulette and are aware of the possibility of misinterpreting them.
This guide will familiarize you with roulette probabilities, payout odds, and house edge, providing a trustworthy source for their numerical values.
The guide covers the most popular versions of roulette: American, European, and French roulette.
Here’s what you will learn:
Let’s get started.
First, you have to know that there is not much difference between the three versions of roulette concerning rules and payout schedule.
These versions somewhat differ in the design of the betting table and the extra number (00) that the American Roulette has on its wheel and table.
Instead, the probabilities associated with the bets and house edges are different across the versions, as we shall see in a further section.
A simple bet in roulette is defined as a bet that is made through a unique placement of chips on the roulette table.
For instance, a split bet is a simple bet made through one placement of chips on the common edge of two adjoining squares on the table; like that on 4 and 5, or 6 and 9 and so on.
There are two categories of simple bets – inside bets and outside bets. The name pertains to the position of the zone marked for the bet on the table relative to the grid of numbers.
Payout odds are the rate at which the stake of a simple bet you win is paid back to you along with your initial stake and are expressed in the form of odds.
For example, the payout odds of a column bet is 2:1, meaning you are paid back twice your stake if you win it.
There are 10 kinds of simple bets, which are listed in the tables below along with their payout odds and possible number of placements:
The payout odds above apply to any of the three versions of roulette.
The trio and four-numbers bets are specific to French roulette. However, several casinos allow such bets in European or American roulette.
In the split row, the number depends on each casino’s rules regarding a split bet with the number 0 or 00.
For example
If you bet $10 on a street, you have 12 possible choices for placing your chips on the table, and if you win, you are paid back $10 x 11 = $110 plus your initial stake.
A combined (or complex) bet is a bet made of several simultaneous placements, each with its own stake, according to the rules of placement. Hence a combined bet consists of several simple bets.
For a combined bet, the payout is applied as follows: the simple bets that are lost receive no prize, and you lose their stakes and for each simple bet that is won its payout odds apply, per the table above.
For example
Assume you placed a combined bet in European Roulette, consisting of the following simple bets: $10 on Red, $2 on street (10, 11, 12), and $1 straight-up bet on number 21.
Suppose number 12 comes up at the spin. You lose the straight-up bet and get back $10 x 1 + $10 + $2 x 11 + $2 = $44, which means a $32 profit from this bet.
Keep in mind
Payout refers to the profit you make when a bet is won and not the entire amount of money that you receive back from the dealer. This latter also includes your initial stake.
The probabilities of the various outcomes can be computed using the classical formula of probability:
“The probability of an event is the ratio between the number of situations favorable for that event to occur and the total number of equally possible situations.”
This means a simple arithmetical operation, that of division.
Each number on the roulette wheel represents an elementary event and all these events are equally possible in a random spin of the wheel. In terms of probability theory, these numbers form the sample space of the experiment of spinning the roulette wheel.
As such, the probability of a specific number to occur is 1 divided to the total numbers on the wheel, that is:
- 1/37 (2.70%) for the European or French roulette
- 1/38 (2.63%) for the American roulette.
How about the probability of composed events?
A composed event consists of a union (disjunction) of several elementary events.
For example
The event E - “any of the numbers 22, 23, 25, and 26” at a European roulette consists of four elementary events (it is identified with set {22, 23, 25, 26}) and its probability is P(E) = 4/37 (10.81%). Event E is actually the event of winning the corner bet on numbers (22, 23, 25, 26).
In the table below are noted the probabilities of winning for each of the simple bets of roulette in fraction, percentage, and odds formats.
Examples
- A simple bet on numbers 32 and 35 at American roulette is a split bet and has the probability of winning 5.26%;
- A simple bet on the numbers 1 to 12 at European roulette is a dozen bet (1st dozen) and has the probability of winning 32.43%;
- A simple bet on red at French roulette is a color bet and has the probability of winning 48.64%.
We can see in this table that the winning odds are the same for the European and French roulette (and this is obvious since the two versions have the same sample space) and that the winning odds for European/French roulette are slightly higher than those for the American roulette.
The main difference between the roulette wheels comes of course from the fact that the American has one more number on the wheel (the double zero).
By looking at the odds of the simple bets, one can see them increasing with the outside bets and reaching their maximum for the Red/Black, Even/Odd, and Low/High bets (47.36% - 48.64%).
They seem high odds of winning that we don’t find in other casino games, but don’t get excited about this: The odds of winning are not the only thing that counts in describing a bet, as we shall see in a further section.
Roulette rules allow the multiple placements all over the table and in whatever combination, resulting in combined bets. Computing the probability of winning such a bet is as simple as doing it for the simple bets.
The set of numbers that a bet (simple or combined) is made on is called the coverage of that bet (C).
Examples
- A simple street bet on numbers 16, 17, and 18 has the coverage {16, 17, 18}, counting three elements (numbers);
- A simple bet on Black has the coverage {2, 4, 6, 8, 10, 11, 13, 15, 17, 20, 22, 24, 26, 28, 29, 31, 33, 35}, counting 18 elements;
- A combined bet consisting of a split bet on (22, 25) and a bet on the 2nd Dozen has the coverage {13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25}, counting 13 elements.
The probability of winning a combined bet B is the ratio between the cardinality of its coverage (the number of elements in the coverage set or the length of the coverage) and the total number of numbers (37 or 38): P(B) = |C(B) |/37 or P(B) = |C(B)|/38, depending on the roulette version.
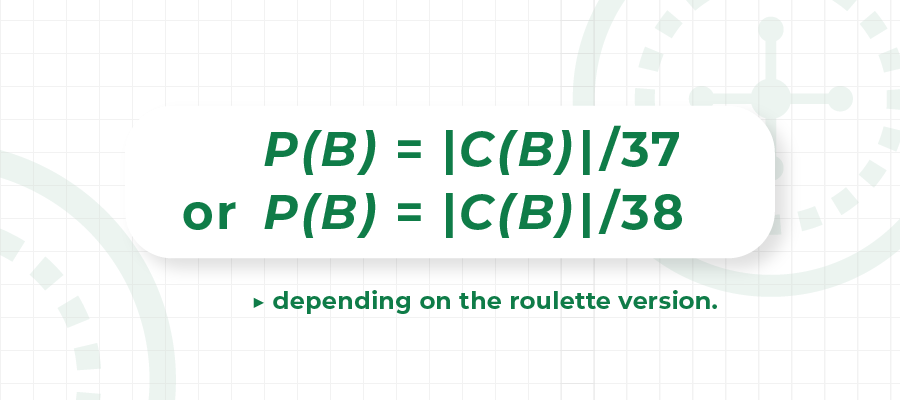
Quick example
Take a bet B at European roulette consisting of the split bets on (4, 5) and (5, 6) and the 2nd Column bet. The coverage of B is C(B) = {2, 4, 5, 6, 8, 11, 14, 17, 20, 23, 26, 29, 32, 35}, counting, 14 elements, its cardinal is |C(B)| = 14, then the probability of winning B is P(B) = 14/37 = 37.83%, while the probability of losing it is 1 – P(B) = 62.17%.
Keep in mind
When computing the probability of winning a combined bet, first establish its coverage by making the union of all coverage of the constituent simple bets. For counting the cardinality of the bet’s coverage, you should count any element only once. Some coverage may overlap (as in the previous example) and any number counts equally for the probability.
Looking at the above formula of probability, one can fairly draw the conclusion that the larger the coverage of a bet, the higher its probability of winning.
But this does not mean that spreading the chips chaotically on the table just to cover as many numbers as possible is a wise betting action.
There are 2 reasons for that:
- We could run into a bet that never wins, no matter the outcome of the spin.
For instance: If you bet the same stake, say, $1 on each of the 38 numbers of an American roulette (38 straight-up bets), this combined bet would have a negative profit of $1 x 35 – $1 x 37 = – $2 whatever the result of the spin. This is true because only one straight-up bet wins and the other 37 such bets lose.
Or, if you bet $1 on each number from 1 to 18 and $18 on High, then: if a number from 1 to 18 occurs, your profit would be $1 x 35 – $1 x 17 – 1 x $18 = 0; if a high number occurred, your profit would be – 1 x $18 – 18 x $1 = – $36, which is negative.
Such combined bets that result in a loss whatever the outcome are called contradictory bets and should be avoided, regardless of their coverage.
Be aware
High probability of winning does not entail a higher profit.
In roulette mathematics, the possible profit of a bet is described by the profit function of that bet, which equates the payouts of the constituent bets.
Roulette is a game such conceived that there is a balance between the probability of winning and the possible profit of a bet relative to the stake – the higher one, the lower the other.
This balance has of course the role of guaranteeing the house advantage and minimizing the risk for the house to go bankrupt.
Keep in mind
Don’t place a combined bet with a large coverage before checking if the bet is not contradictory.
When talking about enhancing the winning odds at a roulette spin, it’s about placing combined bets that offer a higher probability of winning than the simple bets.
Since winning probability increases with the coverage of a bet, choosing large coverage is the only means by which one can obtain greater odds of winning.
This principle also applies in other games of chance (for instance, enabling more paylines in slots or buying more tickets in lottery increase the odds of winning).
Roulette is the casino game providing the highest odds of winning for strategic bets. Check out our beginner's guide if you are not yet familiar with all the bets and combinations.
Combined bets with large coverage may come to reach over 92% odds of winning them and make profit. However, as I already said, probability of winning is not the only factor in the equation of winning at roulette.
Choosing the combined bets to place cannot be done chaotically. We saw that a first requirement is for the bet not to be contradictory, so a check on its possible profit is needed.
Second, there is no objective reason for choosing the constituent bets such that their coverage to overlap, that is, to have numbers covered by more than one bet. In roulette theory, it is proved that any combined bet is equivalent with a combined bet. This means that they have the same length of their coverage and the same values of their profit functions) whose constituent bets do not overlap in coverage (such a bet is called a disjointed bet).
The strategic reasoning for choosing a disjointed bet between two equivalent bets is the following:
By this choice, we can save a portion of the total stake for another bet to be placed at the same spin or for a future spin while keeping the same probability of winning between the two bets.
It’s about saving money relative to the roulette odds of winning.
Keep in mind
For a spin, choosing bets that do not overlap in coverage is better.
Third, enlarging coverage should be done relative to your betting strategy, which also involves bankroll and money management. A high probability of winning is always counterbalanced by a low profit rate, for the house advantage over the long run to be ensured.
For instance
At an American roulette, assume you place the following combined bet: $23 on Red and $1 on each of 12 black numbers. The overall odds of winning this large-coverage bet are about 79%. If you win the color bet, the profit is $11, and if you win a straight-up bet, the profit is only $0.5. If you lose all bets (with about 21% odds), the loss is $35.
We can see that the possible profit is relatively low if we consider the investment of $35.
The profit rate of a bet is the ratio between its stake and the average possible profit in case of a win and counts as another factor in betting decisions along with probability.
There are various strategies of betting with large-coverage combined bets while meeting all or most of the above requirements.
Some known large-coverage bets are in the following categories:
- Betting on a color and on numbers of the opposite color
- Betting on a column and on numbers outside that column
- Betting on the third column and on the color black
- Betting on streets and on the opposite of the predominant color
- Betting on corners and on the opposite of the predominant color
- Betting on lines and on the opposite of the predominant color
- Betting on a color and on splits of the opposite color
- Betting on High/Low and on splits of low/high numbers
- Betting on first and third columns and on the color black.
Each of such combined bets is characterized by parameters that give the probabilities of winning and losing and the profit rate. Before choosing such a bet, it is worth to know these mathematical indicators to see if its fits your goals and betting strategy, including money management.
For example, consider in the list above the combined bet ‘on the third column and on the color black’ in American roulette. This bet derives from the observation that the third column contains more red numbers than either of the other two. By combining the column bet (on the third column) with a bet on the color black, we enlarge the coverage and implicitly increase the probability of winning. The only parameter that characterize this bet is the ratio between the stake on the color bet and that of the column (denote it by c)
Remember
Under the condition of a non-negative profit in the non-losing cases, some simple math work gives a limitation for parameter c, by constraining it to take values in the interval [1, 2].
The following table notes the probabilities and possible profits for this bet, for the various values of c in increments of 0.2. Letter S denotes the stake on the column bet:
With a winning probability of 68.43%, this kind of bet with two placements offers relatively good profit rates for the possible profit.
Its winning probability is about 20% higher than that of a color bet for instance, whose profit rate is about the same with the average rate of the combined bet. These advantages over the color bet are yet counterbalanced by a higher possible loss for the combined bet.
In the previous sections, we have dealt with the odds associated with static bets, that is, bets placed at one single spin. A frequent betting behaviour of many players is to keep the same bet for several spins, with a constant or increasing stake. The latter option is related to progressive betting systems such as the Martingale.
For such bets, one may be interested in what is the probability of a certain succession of outcomes of the same kind or the probability of a certain number of outcomes of the same kind occurring within a given number of spins.
Consider an event A given by the expected outcome of a simple bet (for instance, red color, high number, number 15, 1st column, and so on). After each spin, event A may occur with probability p and not occur with probability 1 – p.
Since the spins are independent, so are the occurrences of event A. Then, the probability of A occurring n times in a row is simply the multiplication:
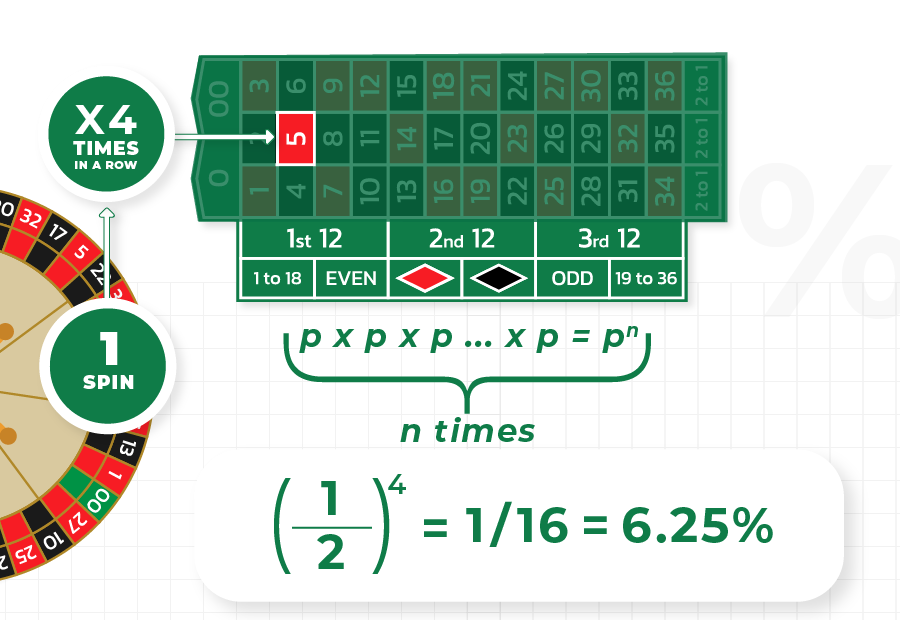
For example
For computing the probability of a red number occurring four times in a row, take the probability for it to occur at one spin and raise it to the power of 4: Let’s approximate its probability at one spin to 1/2, for simplifying the computation (the actual probability is either 48.64% or 47.36%, depending on the roulette version). Then, the sought probability is about 6.25%
Since p is a number less than 1, it follows that the longer the succession, the lower its probability. Actually, the probability decreases exponentially with the number of spins.
The probability of having five reds in a row is 3.12%, and having eight reds in a row gets down to 0.39%.
Such low odds for the repetitions fuel a well-known gambling fallacy – based on the belief that such a succession has to come to a quick end for the randomness to be somehow “restored”.
Such a belief induces the wrong estimation for the probability of a new outcome of the same kind (continuing the succession) to be lower than its actual probability. Such fallacy is called The Monte Carlo Fallacy and affects especially those playing progressive betting systems.
The correct attitude relative to repeated outcomes is to know that every spin is independent of the previous and the probability of an outcome is always the same, regardless of the previous occurrences.
For instance, the probability of a red number occurring at the next spin is about 1/2, no matter how long is the succession of reds until that spin.
The probability for the event A to occur exactly m times in n spins is given by a bit more complex formula, where the first factor is the number of combinations of n elements taken each m:
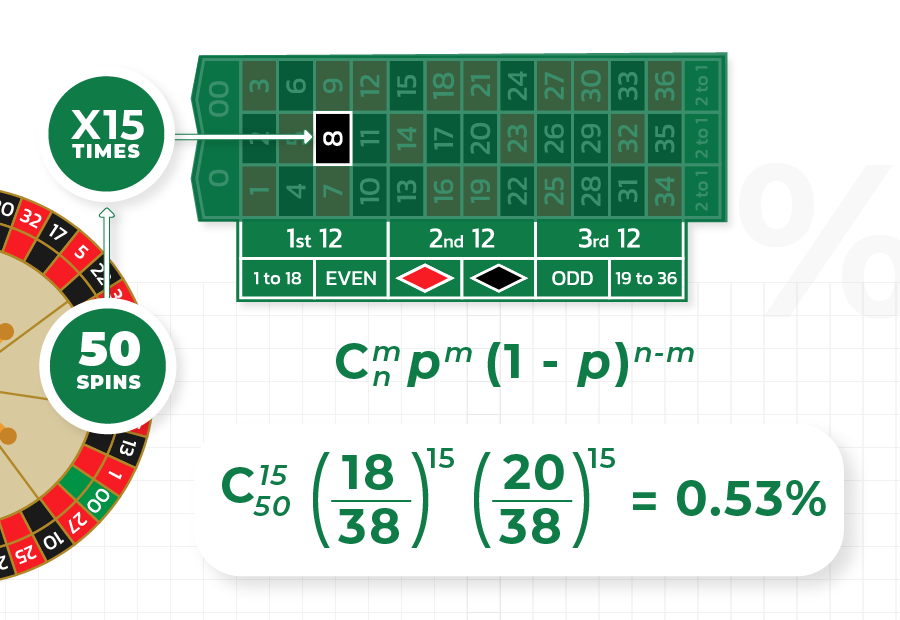
As you can see in the image above, in American roulette, the probability of a black number occurring 15 times in 50 spins is 0.53%.
In American roulette, the probability of a red number occurring at least 7 times in 10 spins is computed as follows: We have to apply the above formula for four times, that is, for m = 7, m = 8, m = 9, and m = 10, and add the results together. This operation gives us a probability of 13.21%.
Keep in mind
Each outcome is independent of the previous and the probability of an outcome does not depend on the previous outcomes nor on the probability of any outcomes of that kind to occur in a row.
The probabilities associated with a bet, together with its payout odds, give what is called the mathematical expectation or expected value of that bet.
In other words the average amount to win or lose over the long run with that bet.
In general, the expected value (EV) of a bet is defined as follows:
(probability of winning) × (payoff if you win) + (probability of losing) × (loss if you lose).

For example, a column bet with a $3 stake at European roulette has an expectation of 12/37 × $6 ˗ 25/37 × $3 = ˗8.1 cents.
This formula employs the probabilities of winning and not winning the bet, the payout of the bet (2 to 1 for the column bet), and the stake. The result reads as follows: If one runs this bet a large enough number of times, they are expected to lose on average 8.1 cents for every three dollars bet or 2.7 cents for every dollar bet.
In probability theory, that “average” means a limit and not actually an arithmetic mean; it is a statistical average.
House edge (HE) of a bet is defined as the opposite (as sign plus or minus) of its expected value. HE is expressed as a percentage and is calculated as the ratio of the average loss to the initial bet. HE expresses the rate of the profit that the house makes over the long run from the players’ loss.
HE is also specific for a game, not only for every bet in that game, and is computed as a statistical average for all the bets in that game.
In our column-bet example in European roulette, HE is 2.70%.
If you consider any other bet for example of calculation (straight-up, split, street, etc.) you will find the same 2.70% for the European roulette.
This happens because the payout schedule of roulette is such chosen to keep the same house edge across the bets.
This does not happen in all the casino games. Most of them have different house edges for their bets. It is another element of simplicity for the roulette game.
Be aware
The house edge of American roulette is almost twice bigger that the HE of the European roulette; it is 5.26%. The HE gets higher because of the additional number 00 that the American roulette has on its wheel.
This difference in HE turns into a straightforward recommendation of choosing the European or French roulette instead of the American roulette.
If we take as a criterion of choosing the probabilities of winning, the difference will still favor European roulette but not so significantly:
For a straight-up bet, the difference in probability of winning is 1/37 – 1/38 = 0.00071 = 0.071%, which is negligible.
The difference gets higher with the coverage of the bet: for a street bet, 3/37 – 3/38 = 0.21%; for a line bet, 6/37 – 6/38 = 0.43%; for a dozen bet, 12/37 – 12/38 = 0.86%, attaining its maximum for a color, even/odd, or low/high bet, namely, 18/37 – 18/38 = 1.28%.
It is still not much, but these latter types of bets are those mostly affected by the zero and double zero, and for American roulette, the chances of losing such a bet are almost doubled.
That 1.28% difference gets even higher for combined bets with high coverage. For instance, a non-contradictory combined bet consisting of a bet on High and seventeen equal straight-up bets on low numbers has a probability of 94.59% in European roulette and 92.10% in American roulette, so the difference jumped to 2.49%.
The only practical reason for choosing the American roulette would actually not be based on HE or probability, but rather on the casino’s particular betting rules.
One such rule would be the permission for lower stakes for particular types of bets in some American roulette casinos.
Remember
European roulette offers higher odds of winning for the same bet and a lower house edge than the American roulette.
In roulette house edge cannot be reduced by using certain betting strategies.
This is possible in blackjack, where optimal strategies reduce the regular house edge, as well as in other games of chance that allow optimal play.
In roulette house edge remains fixed and can only vary with the game’s rules that determine the versions of this game.
There are two rules which impact house edge.
They are mostly specific to French roulette, but some casinos included also them for the other types of roulette. These rules apply when the ball lands in the zero pocket:
The La Partage rule states that if the ball lands in the zero pocket, all even-money wagers (for Red/Black, High/Low, and Odd/Even bets) are automatically split in half.
Half of the original stake will be returned to the player while the house takes the remaining half.
The En Prison rule states that for an even-money wager, if the ball lands on zero, the stake is frozen and a free re-spin will determine if the bet is won or lost.
La Partage and En Prison rule only apply for the even-money bets (1:1 payout odds) and are not present both in a game.
For such bets, the house edge is 1.35% instead of 2.70%.
This house edge is just for that kind of bet for which one of the two rules above applies; for the rest of the bets, the same 2.70% house edge stands.
Hence the overall house edge of the game is not reduced to 1.35%.
Assuming a uniform distribution of the kinds of bets over the long run, the house edge of a French roulette with one of the La Partage or En Prison rules is 2.66%.

| Bet | House Edge |
| Any bet in classical European roulette | 2.70% |
| Any bet in classical American roulette | 5.26% |
| Non even-money bet in French roulette | 2.70% |
| Even-money bet in French roulette with La Partage or En Prison | 1.35% |
| Roulette Version | Overall House Edge |
| European roulette | 2.70% |
| American roulette | 5.26% |
| French roulette | 2.66% |
Remember
The house edge of the French roulette is slightly lower than that of the European roulette, but only if you place even-money bets.
Conclusion
Roulette is a game whose basic mathematical aspects are easy to understand and memorize. I recommend checking the Roulette Academy guides to familiarize yourself with the basics.
Winning roulette odds associated with any bet are computed as the ratio between the length of the coverage of that bet (how many numbers does the bet cover) and the total number of numbers on the wheel (37 or 38).
House edge of roulette can only take three values, depending on version. House edge is fixed and cannot be reduced by playing optimal strategies.
The best roulette betting strategy available is enlarging the overall coverage of the static bets or playing progressive systems.
For the former, increasing winning odds is done with the cost of lowering the profit rate in case of a win. For the latter, the same principle applies and in addition bankroll is essential.
In roulette, like in other games of chance, there is a balance between winning odds, profit rate and expectation and no objective strategy can take into account only one factor or another, but all together.

Bonuses
Casinos
Games
Academy
News
Shop
NEW Q&A
Sweepstakes